自动摘要: 矩阵定义由m×n个数aij排成的m行n列的数表称为m行n列的矩阵,简称m×n矩阵。记作:
这m×n 个数称为矩阵A的元素,简称为元,数aij位于矩阵A的第i行第j列,称为矩阵A的(i , j)元,以数 aij为(i , j)元的矩阵可记为(aij)或(aij)m × n,m×n矩阵A也记作Amn 。元素是实数的矩阵称为实矩阵,元素是复数的矩阵称为复矩阵。而行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵。矩阵类型
- 方阵:行数与列数都等于n的矩阵称为n阶矩阵(也叫n阶方阵),n阶矩阵A也记作An
- 行矩阵:只有一行的矩阵,称为行矩阵,也叫行向量,A=(A1A2…An)
- 列矩阵:只有一列的矩阵,称为列矩阵,也叫列向量
- 同型矩阵:两个矩阵的行数相等,列数也相等,称它们为同型矩阵,如果矩阵A和B的对应元素相等,那么就称矩阵A和矩阵B相等,记作A=B
- 零矩阵:元素都是零的矩阵称为零矩阵,记作0,注意不同型的零矩阵是不同的(因为矩阵的行列数不同)
- 对角矩阵:从左上角到右下角的直线(叫做对角线)以外的元素都是0
- 单位矩阵:对角矩阵中对象线上的元素都是1,其他元素都是0,这种矩阵叫做单位矩阵,简称单位阵
- 对称矩阵:设A为n阶方阵,如果aij=aij(i,j=1,2,…,n),那么A称为对称矩阵,简称对称阵,对称矩阵的特点是:它的元素以对角线为对称轴对应相等。
矩阵的基本运算加、减法:相同的位置数字进行加、减运算。数乘:矩阵乘以一个常数,就是所有位置都乘以这个数乘法: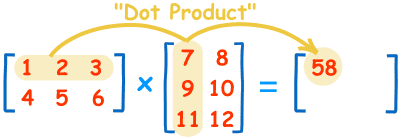
也就是说,结果矩阵第m行与第n列交叉位置的那个值,等于第一个矩阵第m行与第二个矩阵第n列,对应位置的每个值的乘积之和。💡可以从线性方程式的角度理解矩阵乘法严格证明:有三组未知数x,y,t,其中x和y的关系如下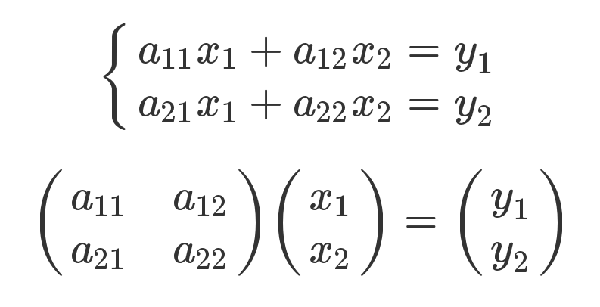
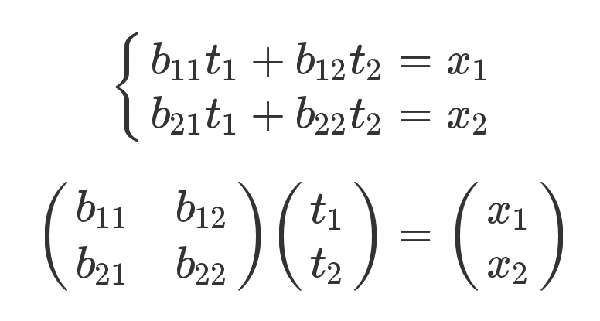
仿射变换
- 仿射变换的两个特点
- 变换前是直线,变换后依然是直线
- 直线比例保持不变
- 放射变换是:线性变换+“平移”
图形变换的矩阵方法
- 旋转矩阵
1. - 缩放矩阵
- 平移矩阵
使用矩阵对3D对象进行位置设置
- 正常使用three.js的时候,都是通过模型上的position、rotation、scale进行设置模型位置,three.js通过这三种一次操作先进行缩放然后旋转最后确定位置。
- three.js内部实现了矩阵的使用,可以通过矩阵的方法实现对模型的变换。
- 任何3D物体Object3D都有三个关联的矩阵:
- Object3D.matrix:储存物体的本地变换,这是对象相对于其父对象的变换
- Object3D.matrixWorld:对象的全局或世界变换。如果对象没有父对象,那么这与存储在矩阵matrix中的本地变换相同
- Object3D.modelViewMatrix:表示对象坐标相对于摄像机空间坐标的转换,一个对象的modelViewMatrix是物体世界变换矩阵乘以摄像机相对于世界空间变换矩阵的逆矩阵。
- 摄像机Camera有两个额外的四维矩阵
- Camera.matrixWorldInverse:视矩阵-摄像机世界坐标变换的逆矩阵
- Camera.projectionMatrix:表示将场景中的信息投影到裁剪空间
- 通过矩阵设置Object3D对象位置:Three.js给我们封装了一个方法,THREE.Matrix4.decompose(Object3D.position, Object3D.quaternion, Object3D.scale),用于更新模型的位置。
- threejs矩阵内部储存形式为列主序
样条曲线
基本概念
样条曲线(Spline Curves):是给定一系列控制点而得到的一条曲线,曲线形状由这些点控制。一般分为插值样条和拟合样条。插值:在原有数据点上进行填充生成曲线,曲线比经过原有数据点拟合:依据原有数据点,通过参数调整设置,使得生成曲线与原有点差距最小(最小二乘),因此曲线未必会经过原有数据点。

