自动摘要: 0预备 pytorch文档官网：[https://pytorch.org/tutorials/beginner/basics/data_tutorial.html](https://pytor ……..

0 预备

pytorch文档官网：https://pytorch.org/tutorials/beginner/basics/data_tutorial.html中文官方文档(翻译的不是pytorch最新版本)：https://pytorch.apachecn.org/#/docs/1.7/07

Anaconda安装

Conda官方文档：https://docs.conda.io/projects/conda/en/latest/commands/config.html#Config%20SubcommandsAnaconda下载网址：https://www.anaconda.com/products/distribution

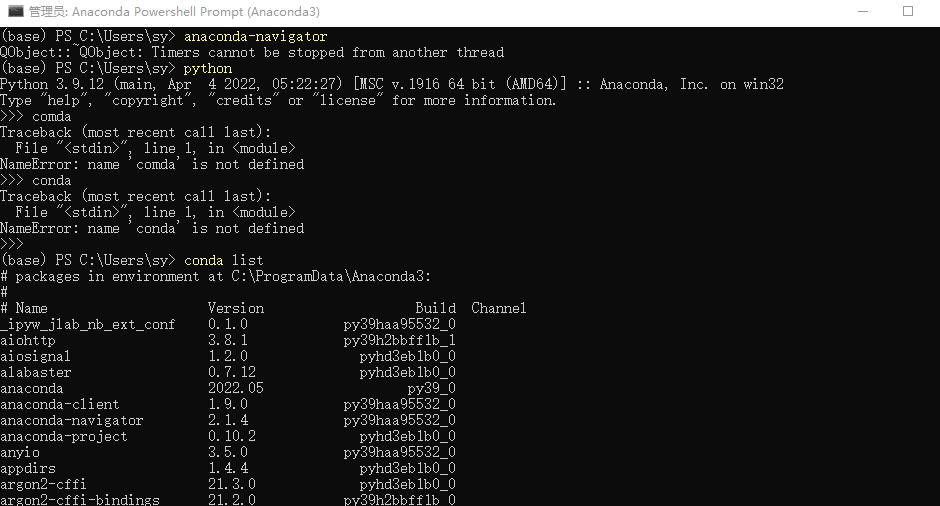
安装完成之后，从“开始”菜单中，单击“Anaconda Powershell Prompt”桌面应用。在命令行中输入”python”，回车进入python编辑中，退出按快捷键Ctrl+z。

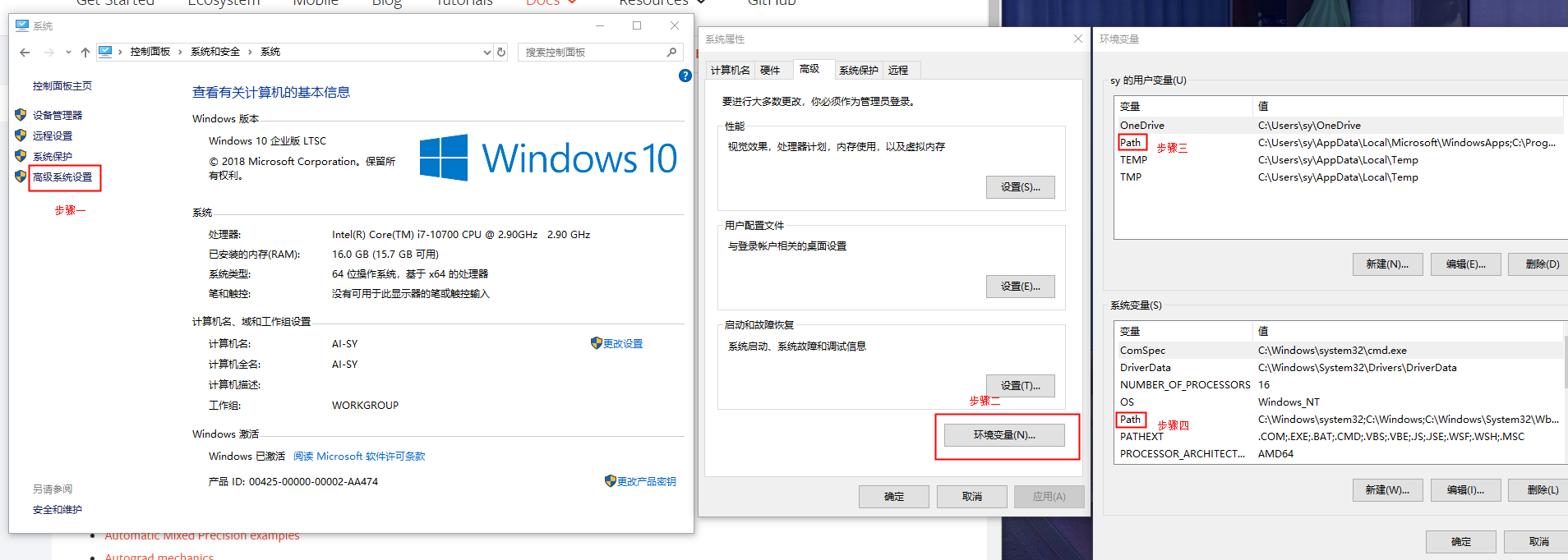
配置环境变量：目的是为了在cmd中可以使用conda。打开控制面板 –> 系统和安全 –> 系统 –> 高级设置 –> 环境变量 –> 分别设置上下两个Path：
双击Path –> 新建：把Anaconda3\Scripts文件路径添加C:\ProgramData\Anaconda3\Scripts –> 点击确定

conda进入base基本环境

安装了 Anaconda 之后，打开 cmd ，输入 Python 之后，提示 Python 不是内部或外部命令，但是在 Anaconda Powershell Prompt中可以正常运行解决方式：Win+R ，输入 cmd ，回车，输入

1	conda info --envs

然后选择一个环境，输入

1	activate xxx

例如，输入

1	activate base

再输入python就可以用了
于是，cmd 中就能正常运行 Python 了。

conda退出base环境及其常用命令

退出当前base环境

1	conda deactivate

常用命令：

#创建一个名为pytorch的环境，指定Python版本是3.9
conda create --name pytorch python=3.9

#查看当前拥有的所有的环境
conda info -e

#环境切换，切换到名为pytorch的环境
source activate pytorch
conda activate YourEnvs (第一个命令无效时使用)

#删除一个名为pytorch的环境
conda remove --name pytorch --all

#安装python包
conda install 包名
conda install -n 环境名 包名
#如果不用-n指定环境名称，则被安装在当前活跃环境
#也可以通过-c指定通过某个channel安装

#查看当前环境下已安装的包
conda list

#查看某个指定环境的已安装包
conda list -n 环境名

#查找包信息
conda search 包名

#更新package
conda update -n 环境名 包名

#删除package
conda remove -n 环境名 包名

#更新conda，保持conda最新
conda update conda

#更新anaconda
conda update anaconda

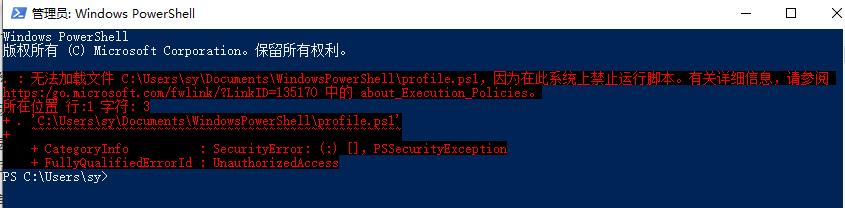
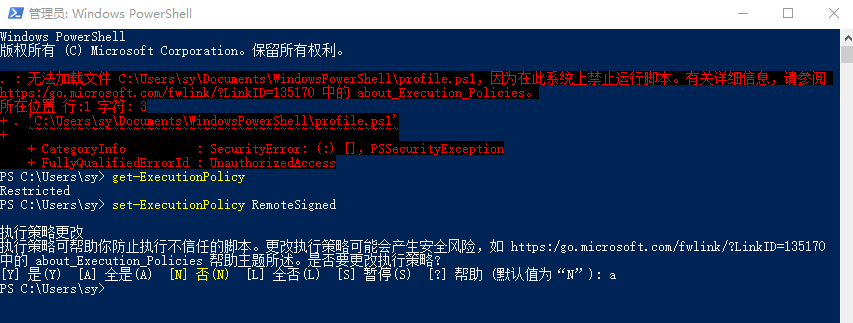
管理员windows powershell进入base环境

打开管理员windows powershell，输入如下代码，回车

1	conda init powershell

关闭后重新打开powershell，若在命令行最前面出现“（base）”，则成功；否则，若出现红色如下警告提示：

1	无法加载文件C:\XXX\WindowsPowerShell\profile.ps1，因为在此系统上禁止运行脚本

执行命令：

1	get-ExecutionPolicy

若回复 Restricted，表示状态是禁止的。执行命令：

1	set-ExecutionPolicy RemoteSigned

将出现如下几个选项，输入 Y（或A）并回车，设置完毕。
重新打开powershell，即可看到命令行开头有“（base）”。

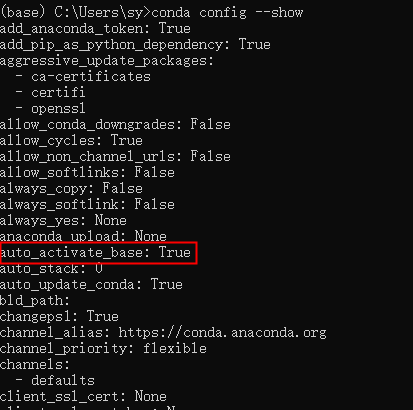
取消打开管理员就进入conda base环境的方法：

方法一：在终端cmd中修改配置：在终端输入conda config –show，会显示所有的配置信息。注意到有：
用conda config –set来修改此配置：

1	conda config --set auto_activate_base false

重启终端即可

方法二：修改配置文件在用户路径下（一般为C:\users\username，linux的话就是/home/username路径）有一个名为.condarc的文件，是conda的配置信息。本机路径是C:\users\sy打开之后是这样的：

channels:
  - http://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/free/
  - http://mirrors.tuna.tsinghua.edu.cn/anaconda/cloud/conda-forge/
  - http://mirrors.tuna.tsinghua.edu.cn/anaconda/cloud/msys2/
ssl_verify: true
show_channel_urls: true

在里面添加一句：auto_activate_base: false 保存即可。

sudo安装

Windows系统命令行使用sudo安装，提示“不是内部命令”，解决方案：新建一个文本文件，将下面代码复制粘贴到文件中，并重命名文本文件为 sudo.vbs （注意后缀改成了 .vbs）。将 sudo.vbs 所在路径添加到环境变量 PATH 中，这样就可以在任意路径下使用 sudo 命令获取管理员权限了。

'ShellExecute 方法  
  
'作用: 用于运行一个程序或脚本。  
  
'语法  
'      .ShellExecute "application", "parameters", "dir", "verb", window  
'      .ShellExecute 'some program.exe', '"some parameters with spaces"', , "runas", 1  
  
'关键字  
'   application   要运行的程序或脚本名称  
'   parameters    运行程序或脚本所需的参数  
'   dir           工作路径，若未指定则使用当前路径  
'   verb          要执行的动作 (值可以是 runas/open/edit/print)  
'                   runas 动作通常用于提升权限  
'   window        程序或脚本执行时的窗口样式 (normal=1, hide=0, 2=Min, 3=max, 4=restore, 5=current, 7=min/inactive, 10=default)  
  
  
Set UAC = CreateObject("Shell.Application")  
Set Shell = CreateObject("WScript.Shell")  
If WScript.Arguments.count<1 Then  
    WScript.echo "语法:  sudo <command> [args]"  
ElseIf WScript.Arguments.count=1 Then  
    UAC.ShellExecute WScript.arguments(0), "", "", "runas", 1  
'    WScript.Sleep 1500  
'    Dim ret  
'    ret = Shell.Appactivate("用户账户控制")  
'    If ret = true Then  
'        Shell.sendkeys "%y"          
'    Else  
'        WScript.echo "自动获取管理员权限失败，请手动确认。"  
'    End If  
Else  
    Dim ucCount  
    Dim args  
    args = NULL  
    For ucCount=1 To (WScript.Arguments.count-1) Step 1  
        args = args & " " & WScript.Arguments(ucCount)  
    Next  
    UAC.ShellExecute WScript.arguments(0), args, "", "runas", 5  
End If

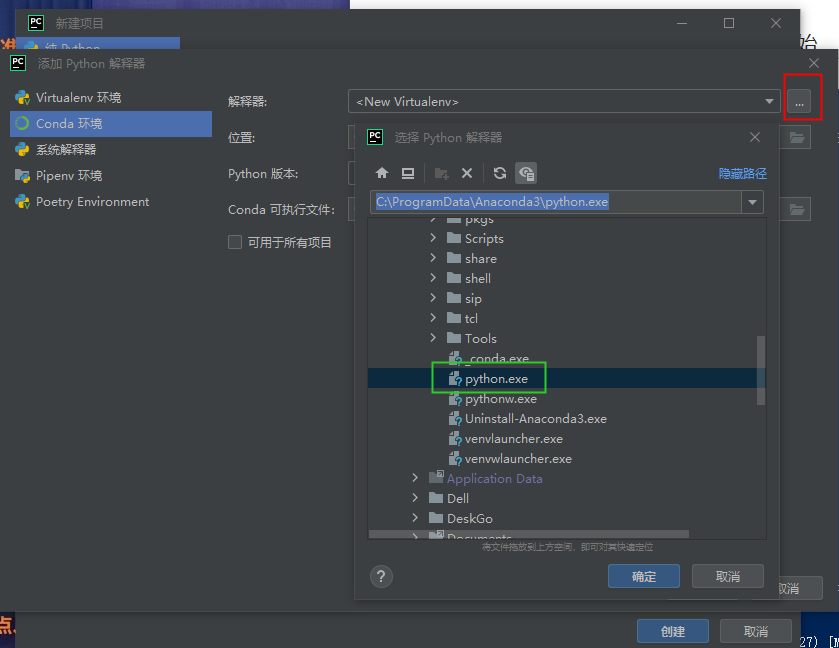
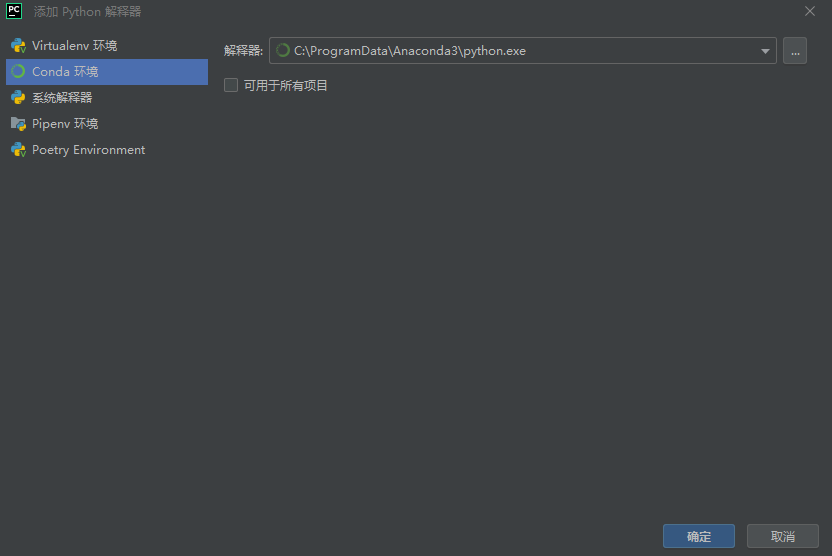
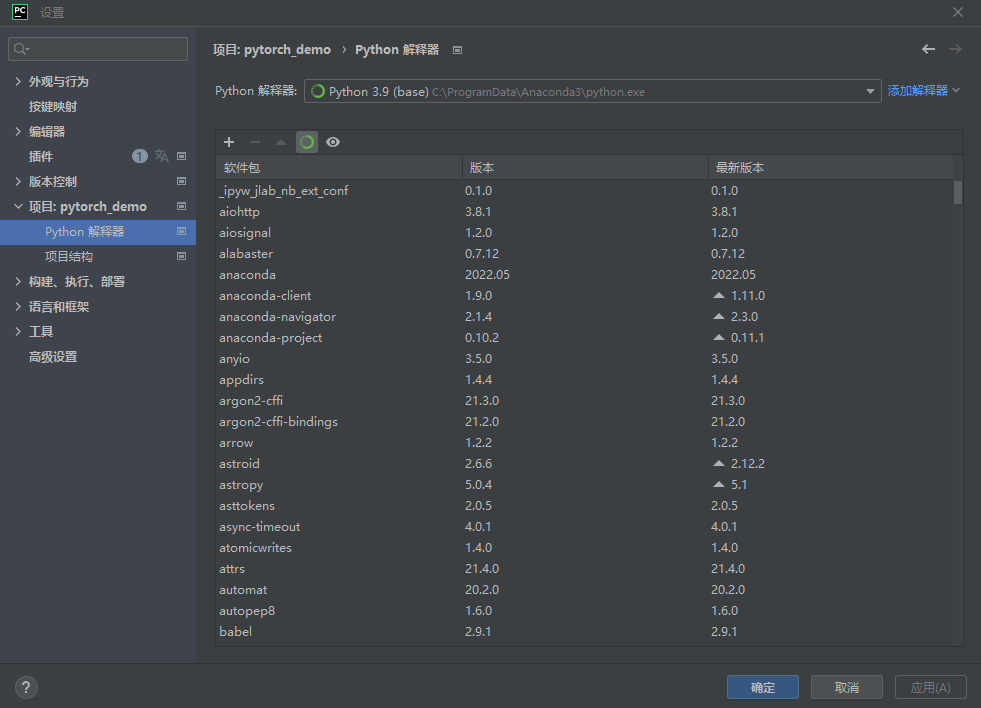
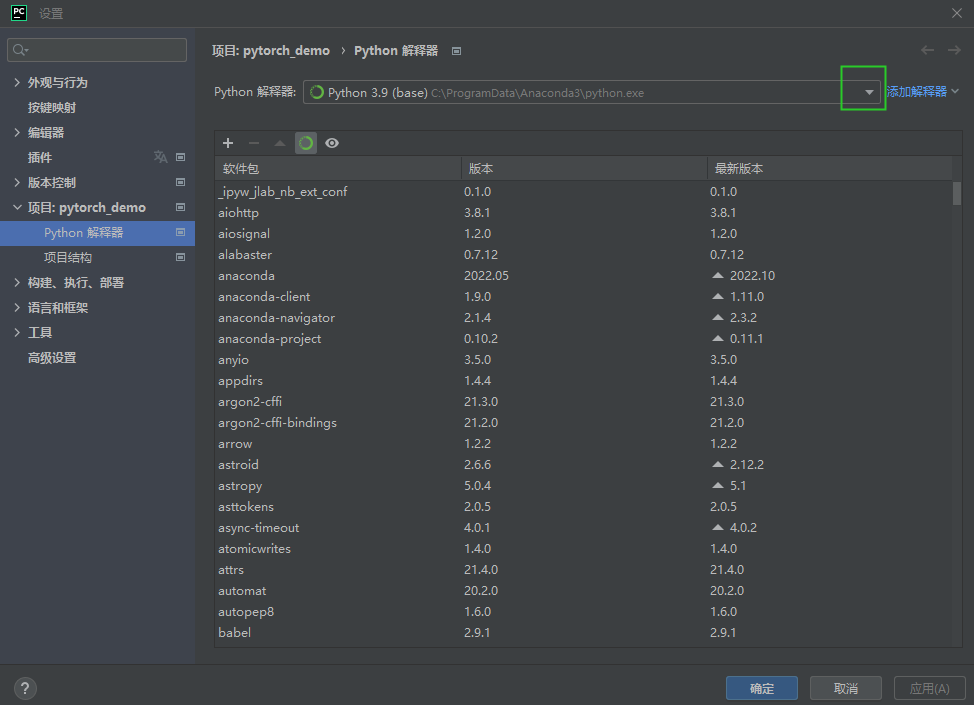
pycharm配置设置

解析器选择的是本地base环境：
点击确定：
在项目中更改：文件–>设置，找到如下图所示的地方更改：
项目存放位置：

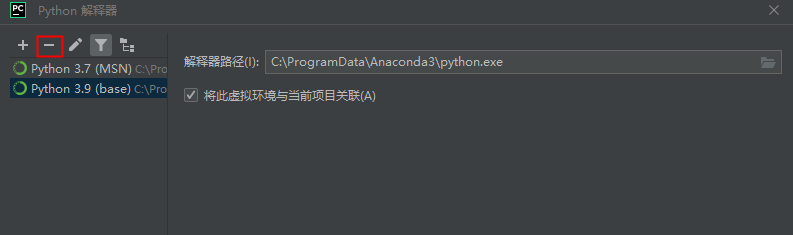
pycharm中删除已有的python解析器：

文件–>设置–>点击找到如下绿色框中的下拉列表框
点击后有全部显示，选中所要删除的环境，点击红色框中’-‘减号：

python面向对象

类定义

语法格式如下：

class ClassName:
    <statement-1>
    .
    .
    .
    <statement-N>

类实例化后，可以使用其属性，实际上，创建一个类之后，可以通过类名访问其属性。

类对象和init

类对象支持两种操作：属性引用和示例化；属性引用使用和python中所有的属性引用一样的标准语法：obj.name；类对象创建后，类命名空间中所有的命名都是有效属性名。所以如果类定义是这样：

#!/usr/bin/python3

class MyClass:
    #简单创建一个实例
    i = 12345
		#创建一个方法
    def f(self):
        return "hello world"

#实例化类
x = MyClass()

#访问类的属性和方法
print("MyClass类的属性 i 为：",x.i)
print("MyClass类的方法f输出为：",x.f())

输出结果：

1 2	MyClass类的属性 i 为： 12345 MyClass类的方法f输出为： hello world

以上创建一个新的类实例并将该对象赋给局部变量x，x为空的对象。

类有一个名为__init__()的特殊方法（构造方法），该方法在类实例化时会自动调用，像下面这样：

1 2	def __init__(self): self.data = [1,2]

类定义了__init__()方法，类的实例化操作就会自动调用__init__()。如下实例化类MyClass，对应的__init__()方法就会被调用：

1 2	x = MyClass() print(x.data)

输出结果：

[1, 2]

当然，init()方法可以有参数，参数通过__init__()传递到类的实例化操作上。例如：

#!/usr/bin/python3

class Complex:
    def __init__(self,realpart,imagpart):
        self.r = realpart
        self.i = imagpart
x = Complex(3.0, -4.5)
print(x.r, x.i)

输出结果：

3.0 -4.5

一定要用__init__()方法吗，不一定，例：

class Rectangle():
    def getPeri(self,a,b):
        return (a + b)*2

    def getArea(self,a,b):
        return a*b


rect = Rectangle()
print(rect.getPeri(3,4))
print(rect.getArea(3,4))
print(rect.__dict__)

输出结果：

1
2
3

14
12
{}

从上例中可以看到，类中并没有定义init()方法，但是也能够得到类似的要求，结果返回了矩形实例rect的周长及面积。但是，我们通过print(rect.dict)来看这个实例的属性，竟然是空的，我定义了一个矩形，按理来说它的属性应该是它的长、宽，但是它竟然没有，这就是没有定义init()的原因了。并且，在实例化对象的时候，rect = Rectangle()参数为空，没有指定a、b的值，只有在调用函数的时候才指定了。且类中定义的每个方法的参数都有a、b，这显然浪费感情，在类中直接指定方法就可以了。因此，需要在类中定义init()方法，方便创建实例的时候，需要给实例绑定上属性，也方便类中方法（函数）的定义。上面例子用采用init()方法定义类，如下：

class Rectangle():
    def __init__(self,a,b):
        self.a = a
        self.b = b

    def getPeri(self):
        return (self.a + self.b)*2

    def getArea(self):
        return self.a * self.b


rect = Rectangle(3,4)
print(rect.getPeri())
print(rect.getArea())
print(rect.__dict__)

输出结果：

1
2
3

14
12
{'a': 3, 'b': 4}

self代表类的实例，而非类

类的方法与普通的函数只有一个特别的区别—-他们必须有一个额外的第一个参数名称，按照惯例他的名称是self。

#!/usr/bin/python3

class Test:
    def prt(self):
        print(self)
        print(self.__class__)

t = Test()
t.prt()

输出结果：

1 2	<__main__.Test object at 0x0000024D70959FD0> <class '__main__.Test'>

从执行结果可以很明显的看出，self代表的是类的实例，代表当前对象的地址，二self.class则转向类。

self不是python关键字，我们把它换成x也是可以正常执行的：

#!/usr/bin/python3

class Test:
    def prt(x):
        print(x)
        print(x.__class__)

t = Test()
t.prt()

输出结果：

1 2	<__main__.Test object at 0x000001D097EA9FD0> <class '__main__.Test'>

类的方法

在类的内部，使用def关键字来定义一个方法，与一般函数定义不同，类方法必须包含参数self，且为第一个参数，self代表的是类的实例。

#!/usr/bin/python3

#类定义
class people:
    #定义基本属性
    name = ''
    age = 0
    #定义私有属性，私有属性在类外部无法直接进行访问
    __weight = 0
    #定义构造方法
    def __init__(self,n,a,w):
        self.name = n
        self.age = a
        self.__weight = w
    def speak(self):
        print("%s 说：我 %d 岁。" %(self.name,self.age))

#实例化类
p = people("runoob",10,30)
p.speak()

输出结果：

1	runoob 说：我 10 岁。

将上面代码进行如下更改

#!/usr/bin/python3

#类定义
class people:
    # #定义基本属性
    # name = ''
    # age = 0
    # #定义私有属性，私有属性在类外部无法直接进行访问
    # __weight = 0
    #定义构造方法
    def __init__(self,n,a,w):
        self.name = n
        self.age = a
        self.__weight = w
    def speak(self):
        print("%s 说：我 %d 岁，体重 %d 斤。" %(self.name,self.age,self.__weight))

#实例化类
p = people("runoob",10,60)
p.speak()

输出结果：

1	runoob 说：我 10 岁，体重 60 斤。

继承

派生类(子类)的定义如下：

class DerivedClassName(BaseClassName):
    <statement-1>
    .
    .
    .
    <statement-N>

子类（派生类DeriveaClassName）会继承父类（基类BaseClassName）的属性和方法。BaseClassName(实例中的基类名)必须与派生类定义在一个作用域内。除了类，还可以用表达式，基类定义在另一个模块中时这一点非常有用：

1	class DerivedClassName(modname.BaseClassName):

实例：

#定义类
class people:
    #定义基本属性
    name = ''
    age = 0
    #定义私有属性，私有属性在类外部无法直接进行访问
    __weight = 0
    #定义构造方法
    def __init__(self,n,a,w):
        self.name = n
        self.age = a
        self.__weight = w
    def speak(self):
        print("%s 说：我 %d 岁。" %(self.name,self.age))

#单继承示例
class student(people):
    grade = ''
    def __init__(self,n,a,w,g):
        #调用父类的构函
        people.__init__(people,n,a,w)
        self.grade = g
    #覆写父类的方法
    def speak(self):
        print("%s 说：我 %d 岁了，我在读 %d 年级"%(self.name,self.age,self.grade))


s = student('ken',10,60,3)
s.speak()

输出结果：

1	ken 说：我 10 岁了，我在读 3 年级

多继承

python同样有限的支持多继承形式。多继承的类定义如下：

class DerivedClassName(Base1, Base2, Base3):
    <statement-1>
    .
    .
    .
    <statement-N>

需要注意圆括号中父类的顺序，若是父类中有相同的方法名，而在子类使用时未指定，python从左至右搜索，即方法在子类中未找到时，从左至右查找父类中是否包含方法。

实例：

#定义类
class people:
    #定义基本属性
    name = ''
    age = 0
    #定义私有属性，私有属性在类外部无法直接进行访问
    __weight = 0
    #定义构造方法
    def __init__(self,n,a,w):
        self.name = n
        self.age = a
        self.__weight = w
    def speak(self):
        print("%s 说：我 %d 岁，体重 %d 斤。" %(self.name,self.age,self.__weight))

#单继承示例
class student(people):
    grade = ''
    def __init__(self,n,a,w,g):
        #调用父类的构函
        people.__init__(people,n,a,w)
        self.grade = g
    #覆写父类的方法
    def speak(self):
        print("%s 说：我 %d 岁了，我在读 %d 年级"%(self.name,self.age,self.grade))

#另一个类，多重继承之前的准备
class speaker():
    topic = ''
    name = ''
    def __init__(self,n,t):
        self.name = n
        self.topic = t
    def speak(self):
        print("我叫 %s ，我是一个演说家，我演讲的主题是 %s"%(self.name,self.topic))

#多重继承
class sample(speaker,student):
    a = ''
    def __init__(self,n,a,w,g,t):
        student.__init__(self,n,a,w,g)
        speaker.__init__(self,n,t)

test = sample("Tim",25,80,4,"Python")
test.speak()    #方法名相同，默认调用的是在括号中参数位置排前父类的方法

输出结果：

1	我叫 Tim ，我是一个演说家，我演讲的主题是 Python

方法重写

如果父类方法不能满足你的需求，可以在子类重写父类的方法，实例：

#定义父类
class Parent:
    def myMedthod(self):
        print('调用父类方法')

#定义子类
class Child(Parent):
    def myMedthod(self):
        print('调用子类方法')

#子类实例
c = Child()
#子类调用重写方法
c.myMedthod()
#用子类对象调用父类已被覆盖的方法
super(Child,c).myMedthod()    #super()函数是用于调用父类（超类）的一个方法

输出结果：

1 2	调用子类方法调用父类方法

类属性与方法

私有属性：__private_attrs：两个下划线开头，声明该属性为私有，不能在类的外部被使用或直接访问。类内部的方法中使用时self.__private_attrs。

class JustCounter:
    __secretCount = 0   #私有变量
    publicCount = 0    #公开变量

    def count(self):
        self.__secretCount += 1
        self.publicCount += 1
        print(self.__secretCount)

counter = JustCounter()
counter.count()
counter.count()
print(counter.publicCount)
print(counter.__secretCount)    #报错，实例不能访问私有变量

输出结果：

1
2
2
Traceback (most recent call last):
  File "D:\pytorch_demo\re_demo.py", line 183, in <module>
    print(counter.__secretCount)    #报错，实例不能访问私有变量
AttributeError: 'JustCounter' object has no attribute '__secretCount'

类的方法：在类的内部，使用def关键字来定义一个方法，与一般函数定义不同，类方法必须包含参数self，且为第一个参数，self代表的是类的实例。self的名字并不是规定死的，也可以用this，但是最好还是按照约定使用self.

类的私有方法：__private_method：两个下划线开头，声明该方法为私有方法，只能在类的内部调用，不能在类的外部调用。self.__private_method。

class Site:
    def __init__(self,name,url):
        self.name = name    #public
        self.__url = url    #private

    def who(self):
        print('name: ',self.name)
        print('url: ',self.__url)

    def __foo(self):    #私有方法
        print('这是私有方法')

    def foo(self):    #公有方法
        print('这是公有方法')
        self.__foo()

x = Site('菜鸟教程','www.runoob.com')
x.who()      #正常输出
x.foo()      #正常输出
x.__foo()    #报错，外部不能调用私有方法

输出结果：

name:  菜鸟教程
url:  www.runoob.com
这是公有方法
这是私有方法
Traceback (most recent call last):
  File "D:\pytorch_demo\re_demo.py", line 207, in <module>
    x.__foo()    #报错，外部不能调用私有方法
AttributeError: 'Site' object has no attribute '__foo'

类的专有方法：

init : 构造函数，在生成对象时调用
del : 析构函数，释放对象时使用
repr : 打印，转换
setitem : 按照索引赋值
getitem: 按照索引获取值
len: 获得长度
cmp: 比较运算
call: 函数调用
add: 加运算
sub: 减运算
mul: 乘运算
truediv: 除运算
mod: 求余运算
pow: 乘方

运算符重载

python同样支持运算符重载，可以对类的专有方法进行重载，实例：

class Vector:
    def __init__(self,a,b):
        self.a = a
        self.b = b

    def __str__(self):
				#返回一个对象的描述信息
        return 'Vector (%d,%d)' % (self.a ,self.b)

    def __add__(self, other):
        return Vector(self.a + other.a, self.b + other.b)

v1 = Vector(2,10)
v2 = Vector(5,-2)
print(v1 + v2)

输出结果：

1	Vector (7,8)

Matplotlib

官网：https://matplotlib.org/

matplotlib安装

一般安装Anaconda就会安装matplotlib，如果未安装好就用下面命令之一即可：

1 2	conda install matplotlib pip install matplotlib

安装完成后查看是否安装成功，输出版本号：

1 2	import matplotlib print(matplotlib.__version__)

输出结果：

3.5.1

Matplotlib Pyplot

官网：https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.plot.html

pyplot是matplotlib的字库，是常用的绘图模块，能很方便让用户绘制2D图标，提供相应的API。用法：使用import导入pyplot库，并设置一个别名plt。

1	import matplotlib.pyplot as plt

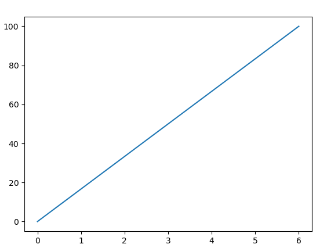
实例：通过两点坐标（0，0）到（0，100）绘制一条线：

import matplotlib.pyplot as plt
import numpy as np

xpoints = np.array([0,6])
ypoints = np.array([0,100])

plt.plot(xpoints,ypoints)
plt.show()

输出结果：
此实例中使用了Pyplot中绘制二维图形的最基本函数plot()。

plot()画图可以绘制点和线，语法格式如下：

# 画单条线
plot([x], y, [fmt], *, data=None, **kwargs)
# 画多条线
plot([x], y, [fmt], [x2], y2, [fmt2], ..., **kwargs)

参数说明：x,y：点或线的节点，x为x轴数据，y为y轴数据，数据可以列表或数组；fmt：可选，定义基本格式（如颜色、标记和线条样式）；**kwargs：可选，用在二维平面图上，设置指定属性，如标签、线的宽度等。

plot(x, y)        # 创建 y 中数据与 x 中对应值的二维线图，使用默认样式
plot(x, y, 'bo')  # 创建 y 中数据与 x 中对应值的二维线图，使用蓝色实心圈绘制
plot(y)           # x 的值为 0..N-1
plot(y, 'r+')     # 使用红色 + 号

颜色字符：’b’ 蓝色，’m’ 洋红色，’g’ 绿色，’y’ 黄色，’r’ 红色，’k’ 黑色，’w’ 白色，’c’ 青绿色，’#008000’ RGB 颜色符串。多条曲线不指定颜色时，会自动选择不同颜色。线形参数：’‐’ 实线，’‐‐’ 破折线，’‐.’ 点划线，’:’ 虚线。标记字符：’.’ 点标记，’,’ 像素标记(极小点)，’o’ 实心圈标记，’v’ 倒三角标记，’^’ 上三角标记，’>’ 右三角标记，’<’ 左三角标记…等等。

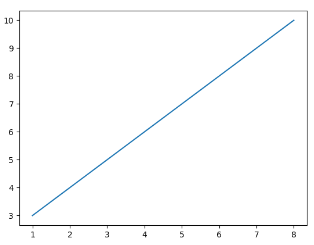
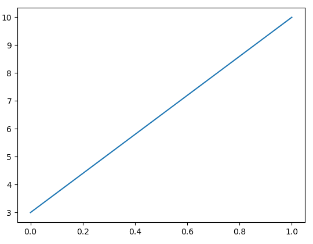
实例：绘制坐标(1,3)到(8,10)的线，我们就需要传递两个数据组[1, 8]和[3, 10]给plot函数：

import matplotlib.pyplot as plt
import numpy as np

xpoints = np.array([1,8])
ypoints = np.array([3,10])

plt.plot(xpoints,ypoints)
plt.show()

输出结果：

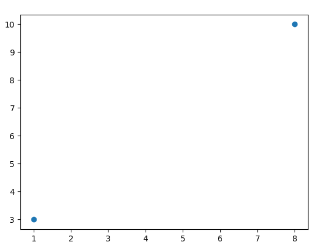
如果只想绘制两个坐标点，而不是一条线，可以使用 o 参数，表示一个实心圈的标记：

import matplotlib.pyplot as plt
import numpy as np

xpoints = np.array([1,8])
ypoints = np.array([3,10])

plt.plot(xpoints,ypoints,'o')
plt.show()

输出结果：

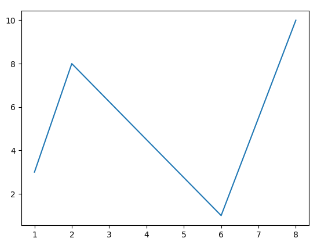
也可以绘制任意数量的点，只需确保两个轴上的点数相同即可。绘制一条不规则线，坐标为(1,3)、(2,8)、(6,1)、(8,10)，对应的两个数组为：[1, 2, 6, 8] 与 [3, 8, 1, 10]。

import matplotlib.pyplot as plt
import numpy as np

xpoints = np.array([1, 2, 6, 8])
ypoints = np.array([3, 8, 1, 10])

plt.plot(xpoints,ypoints)
plt.show()

输出结果：

若不指定x轴上的点，则x会根据y的值来设置为0，1，2，3 … N-1。

import matplotlib.pyplot as plt
import numpy as np

ypoints = np.array([3, 10])

plt.plot(ypoints)
plt.show()

输出结果：

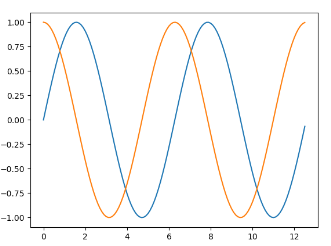
绘制正弦和余弦图，在plt.plot()参数中包含两对x,y值，第一对是x,y，这对应于正弦函数；第二队是x,z，这对应于余弦函数：

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(0,4*np.pi,0.1)    # start,stop,step
y = np.sin(x)
z = np.cos(x)
plt.plot(x,y,x,z)
plt.show()

输出结果：

Matplotlib绘图标记

绘图过程如果我们想要给坐标自定义一些不一样的标记，就可以使用plot()方法的marker参数来定义。

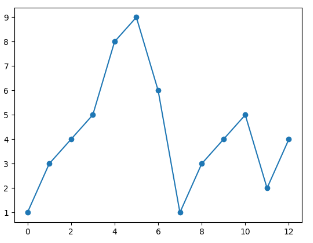
实例：实心圆标记

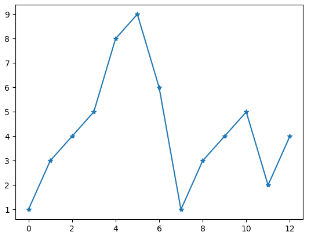
import matplotlib.pyplot as plt
import numpy as np

ypoints = np.array([1,3,4,5,8,9,6,1,3,4,5,2,4])

plt.plot(ypoints,marker = 'o')
plt.show()

输出结果：

marker可以定义的符号如下：

标记	符号	描述
“.”
点
“,”
像素点
“o”
实心圆
“v”
下三角
“^”
上三角
“<”
左三角
“>”
右三角
“1”
下三叉
“2”
上三叉
“3”
左三叉
“4”
右三叉
“8”
八角形
“s”
正方形
“p”
五边形
“P”
加号（填充）
“*”
星号
“h”
六边形 1
“H”
六边形 2
“+”
加号
“x”
乘号 x
“X”
乘号 x (填充)
“D”
菱形
“d”
瘦菱形
“\|”
竖线
“_”
横线
0 (TICKLEFT)
左横线
1 (TICKRIGHT)
右横线
2 (TICKUP)
上竖线
3 (TICKDOWN)
下竖线
4 (CARETLEFT)
左箭头
5 (CARETRIGHT)
右箭头
6 (CARETUP)
上箭头
7 (CARETDOWN)
下箭头
8 (CARETLEFTBASE)
左箭头 (中间点为基准)
9 (CARETRIGHTBASE)
右箭头 (中间点为基准)
10 (CARETUPBASE)
上箭头 (中间点为基准)
11 (CARETDOWNBASE)
下箭头 (中间点为基准)
“None”, “ “ or “”		没有任何标记
‘$…$’
渲染指定的字符。例如 “$f$” 以字母 f 为标记。

实例：*标记

import matplotlib.pyplot as plt
import numpy as np

ypoints = np.array([1,3,4,5,8,9,6,1,3,4,5,2,4])

plt.plot(ypoints,marker = '*')
plt.show()

输出结果：

实例：箭头标记

import matplotlib.pyplot as plt
import matplotlib.markers
plt.plot([1,2,3],marker = matplotlib.markers.CARETDOWNBASE)
plt.show()

结果输出：

fmt参数

fmt参数定义了基本格式，如标记、线条样式和颜色。

1	fmt = '[marker][line][color]'

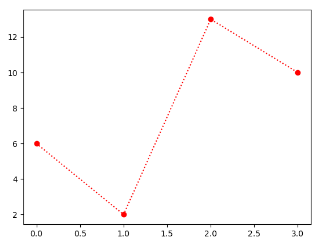
实例：o:r，o表示实心圆标记，：表示虚线，r表示颜色为红色。

import matplotlib.pyplot as plt
import numpy as np

ypoints = np.array([6,2,13,10])

plt.plot(ypoints,'o:r')
plt.show()

输出结果：

线类型：

线类型标记	描述
‘-‘	实线
‘:’	虚线
‘–’	破折线
‘-.’	点划线

颜色类型：

颜色标记	描述
‘r’	红色
‘g’	绿色
‘b’	蓝色
‘c’	青色
‘m’	品红
‘y’	黄色
‘k’	黑色
‘w’	白色

标记大小与颜色：自定义标记的大小与颜色，使用的参数分别是：

markersize，简写为ms：定义标记的大小；
markerfacecolor，简写为mfc：定义标记内部的颜色；
maekerdgecolor，简写为mec：定义标记边框的颜色。

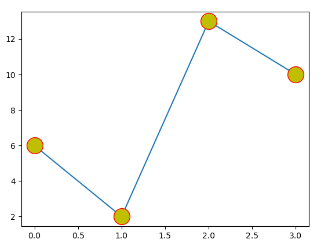
实例：设置标记大小ms=20、标记外边框颜色mec=’r’、标记内部颜色mfc=’y’

import matplotlib.pyplot as plt
import numpy as np

ypoints = np.array([6,2,13,10])

plt.plot(ypoints,marker = 'o',ms = 20, mec = 'r', mfc = 'y')
plt.show()

结果如下：

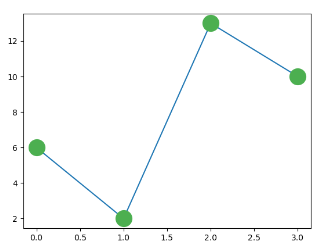
自定义标记内部与边框的颜色：SeaGreen、#8FBC8F 等，完整样式可以参考 HTML 颜色值。

import matplotlib.pyplot as plt
import numpy as np

ypoints = np.array([6,2,13,10])

plt.plot(ypoints,marker = 'o',ms = 20, mec = '#4CAF50', mfc = '#4CAF50')
plt.show()

输出结果：

Matplotlib绘图线

绘图过程需要自定义线的样式，包括线的类型、颜色和大小等。

线的类型

线的类型可以使用linestyle参数来定义，简写为ls。

类型	简写	说明
‘solid’ (默认)	‘-‘	实线
‘dotted’	‘:’	点虚线
‘dashed’	‘–’	破折线
‘dashdot’	‘-.’	点划线
‘None’	‘’ 或 ‘ ‘	不画线

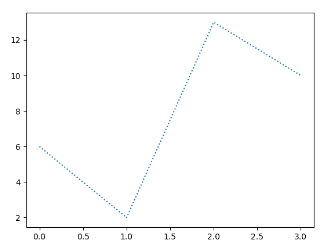
实例：线类型全写linestyle = ‘dotted’

import matplotlib.pyplot as plt
import numpy as np

ypoints = np.array([6,2,13,10])

plt.plot(ypoints,linestyle = 'dotted')
plt.show()

输出结果：

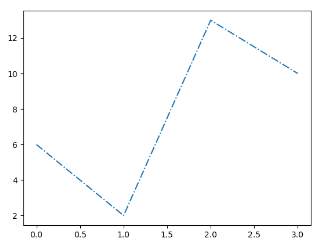
实例：线类型简写ls = ‘-.’

import matplotlib.pyplot as plt
import numpy as np

ypoints = np.array([6,2,13,10])

plt.plot(ypoints,ls = '-.')
plt.show()

输出结果：

线的颜色

线的颜色可以使用color参数来定义，简写为c。颜色类型：

颜色标记	描述
‘r’	红色
‘g’	绿色
‘b’	蓝色
‘c’	青色
‘m’	品红
‘y’	黄色
‘k’	黑色
‘w’	白色

当然也可以自定义颜色类型，例如：SeaGreen、#8FBC8F 等，完整样式可以参考 HTML 颜色值。代码格式：如红色的线color = ‘r’

1	plt.plot(ypoints,ls = '-.',color = 'r')

1	plt.plot(ypoints, c = '#8FBC8F')

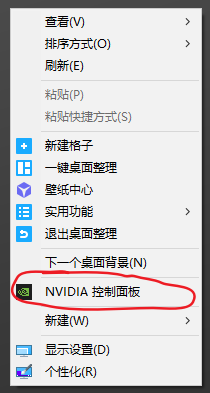
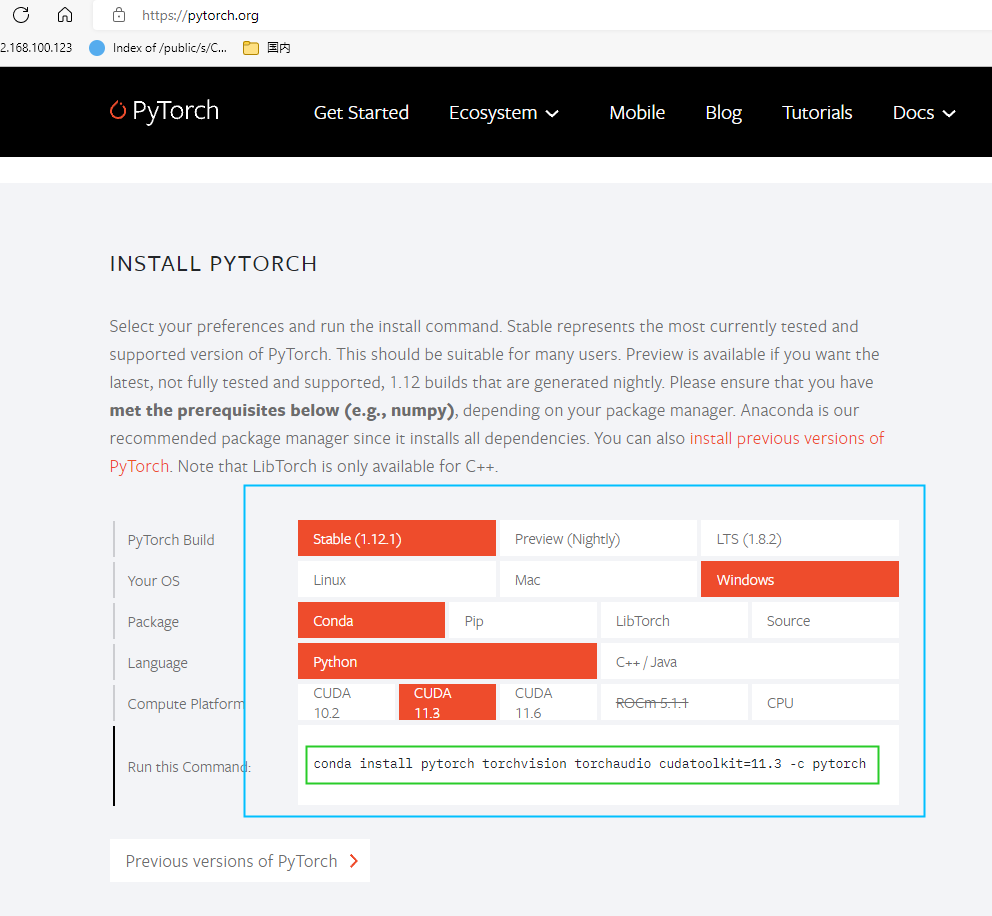
安装pytorch

检查是否有合适的GPU

在桌面上右击如果能找到NVIDA控制面板，则说明该电脑有GPU。本机显然没有：

安装pytorch

官网：https://pytorch.org/，安装教程在首页的Install>
，进入后会有详细的介绍：
由于本机没有GPU，所以选择上图蓝色框内的配置，即在命令行进入指定的环境base（可以新建个环境）内，输入绿色框内命令：

1	conda install pytorch torchvision torchaudio cudatoolkit=11.3 -c pytorch

安装的过程会比较慢。安装完成后进入python，输入以下命令，如果没有报错证明安装成功：

(base) PS C:\Users\sy> python
>>> import torch
>>> x = torch.rand(5, 3)
>>> print(x)
tensor([[0.5715, 0.8384, 0.3018],
        [0.6275, 0.1263, 0.2403],
        [0.3079, 0.2989, 0.6742],
        [0.9151, 0.4709, 0.1775],
        [0.9304, 0.6655, 0.2846]])

也可以在pycharm里面装，之后执行上面代码不报错即可。

1 pytorch简介

1.1 张量

张量是一种特殊的数据结构，与数组和矩阵非常相似。pytorch用张量来编码模型的输入、输出及其模型的参数。

张量与NumPy的ndarrays类似，只是张量可以在GPU或其他硬件加速器上运行。实际上，张量和Numpy数组通常可以共享相同的底层内存，消除了复制数据的需要** **(查阅 Bridge with NumPy)，tensors也优化了自动微分（更多请参考Autograd后面部分），如果熟悉ndarrays，那么你对张量API已经很熟悉了，如果没有，那就跟着做！

1 2	import torch import numpy as np

初始化张量

张量可以用各种方式初始化，看看下面这些例子。

直接从数据中创建

张量可以从数据中创建，数据类型被自动推断出来：

1
2
3

data = [[1,2],[3,4]]
x_data = torch.tensor(data)
print(x_data)

输出结果：

1 2	tensor([[1, 2], [3, 4]])

从Numpy数组中创建

张量可以从Numpy数组中创建（反之亦然，参考Bridge with NumPy）。

1
2
3

np_array = np.array(data)
x_np = torch.from_numpy(np_array)
print(x_np)

输出结果：

1 2	tensor([[1, 2], [3, 4]], dtype=torch.int32)

从其他张量创建

新张量保留了参数张量的属性（形状、数据类型），除非被明确重写。

x_ones = torch.ones_like(x_data)    #保留x_data属性
print(f"one tensor: \n {x_ones} \n")

x_rand = torch.rand_like(x_data,dtype=torch.float)    #覆盖x_data属性
print(f"random tensor: \n {x_rand} \n")

输出结果：

one tensor: 
 tensor([[1, 1],
        [1, 1]]) 

random tensor: 
 tensor([[0.4668, 0.3876],
        [0.0113, 0.6029]])

随机或常量值

形状是张量维度的元组，在下面函数中，它决定了输出张量的维度：

shape = (2,3)
rand_tensor = torch.rand(shape)
ones_tensor = torch.ones(shape)
zeros_tensor = torch.zeros(shape)

print(f"random tensor: \n {rand_tensor}")
print(f"ones tensor: \n {ones_tensor}")
print(f"zeros tensor: \n {zeros_tensor}")

输出结果：

random tensor: 
 tensor([[0.1024, 0.2078, 0.6793],
        [0.8625, 0.4195, 0.1272]])
ones tensor: 
 tensor([[1., 1., 1.],
        [1., 1., 1.]])
zeros tensor: 
 tensor([[0., 0., 0.],
        [0., 0., 0.]])

张量属性

张量属性描述了他们的形状、数据类型和存储他们的设备。

tensor = torch.rand(3,4)
print(f"shape of tensor: {tensor.shape}")
print(f"datatype of tensor: {tensor.dtype}")
print(f"device tensor is stored on: {tensor.device}")

输出结果：

1
2
3

shape of tensor: torch.Size([3, 4])
datatype of tensor: torch.float32
device tensor is stored on: cpu

张量运算

张量运算超过100种，包括包括算术、线性代数、矩阵操作(转置，索引，切片) 及抽样，更多描述请参考** **here。

通常这些运算可以在GPU上运行（通常比CPU上运行速度更快），如果你使用的是Colab，可以分配出一个GPU，步骤： Runtime > Change runtime type > GPU

默认情况下，张量是在CPU上创建的，我们用 .to 方法直接将张量转移到GPU上(确保GPU可用)，跨设备复制大量的张量是非常耗时间和内存的！

1
2
3

# We move our tensor to the GPU if available
if torch.cuda.is_available():
    tensor = tensor.to("cuda")

标准化的numpy类索引和切片

tensor = torch.ones(4,4)
print(f"first row: {tensor[0]}")
print(f"first column: {tensor[:,0]}")
print(f"last column: {tensor[...,-1]}")
tensor[:,1] = 0
print(tensor)

输出结果

first row: tensor([1., 1., 1., 1.])
first column: tensor([1., 1., 1., 1.])
last column: tensor([1., 1., 1., 1.])
tensor([[1., 0., 1., 1.],
        [1., 0., 1., 1.],
        [1., 0., 1., 1.],
        [1., 0., 1., 1.]])

torch.cat可以将一系列张量顺着给定的维度连接起来。参考torch.stack，它是另一个张量连接op，与torch.cat稍有不同。

1 2	t1 = torch.cat([tensor,tensor,tensor],dim=1) print(t1)

输出结果：

tensor([[0., 1., 1., 1., 0., 1., 1., 1., 0., 1., 1., 1.],
        [0., 1., 1., 1., 0., 1., 1., 1., 0., 1., 1., 1.],
        [0., 1., 1., 1., 0., 1., 1., 1., 0., 1., 1., 1.],
        [0., 1., 1., 1., 0., 1., 1., 1., 0., 1., 1., 1.]])

Arithmetic operations算数运算

tensor = tensor = torch.ones(4,4)
tensor[0] = 0
tensor[2] = 2
tensor[3] = 3
print('tensor输出结果:\n',tensor,)

#两个矩阵相乘，y1,y2,y3得出相同的值，其中官网对y3的写法如下：
#y3 = torch.rand_like(y1)
#torch.matmul(tensor, tensor.T, out=y3)
y1 = tensor @ tensor.T
y2 = tensor.matmul(tensor.T)
y3 = torch.matmul(tensor,tensor.T)
print('y3输出结果:\n',y3)

#两个矩阵对应元素相乘，z1,z2,z3得出相同的值，其中官网对z3的写法如下：
#z3 = torch.rand_like(tensor)
#torch.mul(tensor, tensor, out=z3)
z1 = tensor * tensor
z2 = tensor.mul(tensor)
z3 = torch.mul(tensor,tensor)
print('z3输出结果:\n',z3)

输出结果：

tensor输出结果:
 tensor([[0., 0., 0., 0.],
        [1., 1., 1., 1.],
        [2., 2., 2., 2.],
        [3., 3., 3., 3.]])
y3输出结果:
 tensor([[ 0.,  0.,  0.,  0.],
        [ 0.,  4.,  8., 12.],
        [ 0.,  8., 16., 24.],
        [ 0., 12., 24., 36.]])
z3输出结果:
 tensor([[0., 0., 0., 0.],
        [1., 1., 1., 1.],
        [4., 4., 4., 4.],
        [9., 9., 9., 9.]])

Single-element tensors单元张量

如果有一个单元张量，例如将一个张量的所有值聚合成一个值，可以使用item()将其转换为python数值：

tensor = tensor = torch.ones(4,4)
agg = tensor.sum()
agg_item = agg.item()
print(agg_item,type(agg_item))

输出结果：

1	16.0 <class 'float'>

In-place operations就地操作

将结果储存到操作对象中的操作称为就地操作，以 _ 为后缀。例如：x.copy_(y)，x.t_()，将改变 x。

tensor = tensor = torch.ones(4,4)
print(f"{tensor} \n")
tensor.add_(5)
print(tensor)

输出结果：

tensor([[1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.]]) 

tensor([[6., 6., 6., 6.],
        [6., 6., 6., 6.],
        [6., 6., 6., 6.],
        [6., 6., 6., 6.]])

就地操作会节省一些内存，但可能会有问题出现，因为在计算机导数时会立即丢失历史记录，因此不提倡使用。

Bridge with NumPy

CPU上的张量和numpy数组可以共享他们的底层内存位置，改变其中一个另一个也随之改变。

Tensor 到 NumPy array：

t = torch.ones(5)
print(f"t: {t}")
n = t.numpy()
print(f"n: {n}")

输出结果：

1 2	t: tensor([1., 1., 1., 1., 1.]) n: [1. 1. 1. 1. 1.]

改变张量会映射到numpy数组中：

t = torch.ones(5)
n = t.numpy()
t.add_(1)
print(f"t: {t}")
print(f"n: {n}")

输出结果：

1 2	t: tensor([2., 2., 2., 2., 2.]) n: [2. 2. 2. 2. 2.]

1.2 数据集和数据加载器

英文名称：datasets & dataloaders

处理数据样本的代码可能很混乱且难以维护，理想情况下是希望数据集代码与模型训练代码解耦，以获得更好的可读性和模块化。pytorch提供了两个数据基元：torch.utils.data.DataLoader 和 torch.utils.data.Dataset，它允许使用预加载的数据以及计算机本地数据（也就是你自己的数据）。Dataset储存样品及其相应的标签，DataLoader封装了迭代器(iterable)，以便访问Dataset储存的数据。

pytorch提供了许多预加载的数据集（如FashionMNIST），这些数据集对于特定数据的函数进行了子类化torch.utils.data.Dataset和实现化，可以用于原型和测试模型。数据集链接： Image Datasets, Text Datasets 和 Audio Datasets。

数据集加载

下面是如何从TorchVision加载FashionMNIST数据集的示例。Fashion MNIST是Zalando文章图像的数据集，包含6万个示例的训练集和万个示例的测试集。每个示例都是一个28x28灰度图像，与10个类中的一个标签相关联。使用以下参数加载FashionMNIST 数据集：

root是存储训练/测试数据的路径；
train指定训练或测试数据集；
download=True从互联网上下载数据，如果无法在root上找到；

transform和target_transform是指定特征和标签转换。

import torch
from torch.utils.data import Dataset
from torchvision import datasets
from torchvision.transforms import ToTensor
import matplotlib.pyplot as plt


training_data = datasets.FashionMNIST(
    root="data",
    train=True,
    download=True,
    transform=ToTensor()
)

test_data = datasets.FashionMNIST(
    root="data",
    train=False,
    download=True,
    transform=ToTensor()
)

迭代和可视化数据集

我们可以像列表一样手动索引数据集:training_data[index]。我们使用matplotlib将训练数据中的一些样本可视化。

labels_map = {
    0: "T-Shirt",
    1: "Trouser",
    2: "Pullover",
    3: "Dress",
    4: "Coat",
    5: "Sandal",
    6: "Shirt",
    7: "Sneaker",
    8: "Bag",
    9: "Ankle Boot",
}
figure = plt.figure(figsize=(8, 8))
cols, rows = 3, 3
for i in range(1, cols * rows + 1):
    sample_idx = torch.randint(len(training_data), size=(1,)).item()
    img, label = training_data[sample_idx]
    figure.add_subplot(rows, cols, i)
    plt.title(labels_map[label])
    plt.axis("off")
    plt.imshow(img.squeeze(), cmap="gray")
plt.show()

运行结果：

自定义数据集

自定义Dataset类必须满足三个函数： init, len, and __getitem__。看看这个实现；FashionMNIST图像存储在目录img_dir中，它们的标签单独存储在CSV文件annotations_file中。

import os
import pandas as pd
from torchvision.io import read_image
from torch.utils.data import Dataset


class CustomImageDataset(Dataset):
    def __init__(self, annotations_file, img_dir, transform=None, target_transform=None):
        self.img_labels = pd.read_csv(annotations_file)
        self.img_dir = img_dir
        self.transform = transform
        self.target_transform = target_transform

    def __len__(self):
        return len(self.img_labels)

    def __getitem__(self, idx):
        img_path = os.path.join(self.img_dir, self.img_labels.iloc[idx, 0])
        image = read_image(img_path)
        label = self.img_labels.iloc[idx, 1]
        if self.transform:
            image = self.transform(image)
        if self.target_transform:
            label = self.target_transform(label)
        return image, label

init

当实例化Dataset对象时__init__函数就运行一次。我们初始化包含图像、注释文件和两个转换的目录(下一节将详细介绍)。labels.csv文件如下所示：

tshirt1.jpg, 0
tshirt2.jpg, 0
......
ankleboot999.jpg, 9

def __init__(self, annotations_file, img_dir, transform=None, target_transform=None):
    self.img_labels = pd.read_csv(annotations_file)
    self.img_dir = img_dir
    self.transform = transform
    self.target_transform = target_transform

len

__len__函数返回数据集中的样本数量。示例：

1 2	def __len__(self): return len(self.img_labels)

getitem

__getitem__函数从给定索引 idx 处的数据集加载并返回一个示例。基于索引，它识别图像在磁盘上的位置，使用read_image将其转换为一个张量，从self.Img_labels中的csv数据中检索相应的标签，调用其转换函数(如果适用的话)，并返回一个元组中的张量图像和相应的标签。

def __getitem__(self, idx):
    img_path = os.path.join(self.img_dir, self.img_labels.iloc[idx, 0])
    image = read_image(img_path)
    label = self.img_labels.iloc[idx, 1]
    if self.transform:
        image = self.transform(image)
    if self.target_transform:
        label = self.target_transform(label)
    return image, label

用数据加载器数据进行训练

数据集每次检索一个样本的数据集的特征和标签。在训练模型时，我们通常希望以“小批量”传递样本，在每个阶段重新打乱数据以减少模型过拟合，并使用Python的多进程处理来加速数据检索。DataLoader是一个可迭代对象，它通过一个简单的API为我们抽象了这种复杂性。

from torch.utils.data import DataLoader

train_dataloader = DataLoader(training_data, batch_size=64, shuffle=True)
test_dataloader = DataLoader(test_data, batch_size=64, shuffle=True)

循环访问数据加载器

上面已经将该数据集加载到DataLoader中，并可以根据需要遍历该数据集。下面的每次迭代都返回一批train_features和train_labels(分别包含batch_size=64个特性和标签)。因为我们指定了shuffle=True，所以在我们遍历所有批次之后，数据就会被打乱(对于更细粒度的数据加载顺序的控制，请查看Samplers)。

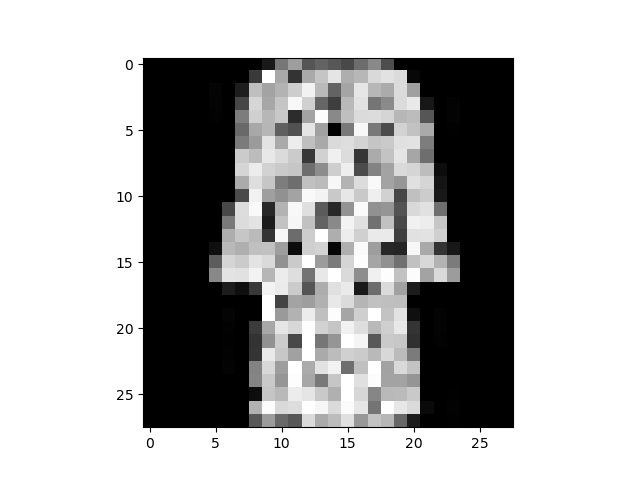
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt
from torchvision import datasets
from torchvision.transforms import ToTensor


training_data = datasets.FashionMNIST(
    root="data",
    train=True,
    download=True,
    transform=ToTensor()
)

test_data = datasets.FashionMNIST(
    root="data",
    train=False,
    download=True,
    transform=ToTensor()
)


train_dataloader = DataLoader(training_data, batch_size=64, shuffle=True)
test_dataloader = DataLoader(test_data, batch_size=64, shuffle=True)
# Display image and label.
train_features, train_labels = next(iter(train_dataloader))
print(f"Feature batch shape: {train_features.size()}")
print(f"Labels batch shape: {train_labels.size()}")
img = train_features[0].squeeze()
label = train_labels[0]
plt.imshow(img, cmap="gray")
plt.show()
print(f"Label: {label}")

输出结果（代码+图片）：

1
2
3

Feature batch shape: torch.Size([64, 1, 28, 28])
Labels batch shape: torch.Size([64])
Label: 3

1.3 Transform

数据并不总是以训练机器学习算法所需的最终处理形式出现，用Transform对数据进行一些处理，使其适合于训练。

所有的 TorchVision 数据集都有两个参数——transform用来修改特征，target_transform用来修改标签——它们接受包含转换逻辑的可调用对象。torchvision.transforms模块提供了几个常用的开箱即用转换。

FashionMNIST特征采用PIL Image格式，标签为整数。在训练中，我们需要特征作为标准化张量，标签是one-hot编码张量，本次用ToTensor和Lambda做这些变换。

import torch
from torchvision import datasets
from torchvision.transforms import ToTensor,Lambda

ds = datasets.FashionMNIST(
    root = "data",
    train = True,
    download = True,
    transform = ToTensor(),
    target_transform = Lambda(lambda y: torch.zeros(10,dtype=torch.float).scatter_(0,torch.trnsor(y),value=1))
)

输出结果：之前没有下载过数据集会输出downloading进度，已经下载过，运行之后没有任何反应。

ToTensor

ToTensor将PIL图像或NumPy ndarray转换为FloatTensor，并缩放图像的像素强度值在范围[0. , 1.]内。

Lambda Transforms

λ-转换适用于任何用户定义的Lambda函数，定义一个函数将整数转换one-hot编码张量。首先创建一个大小为10（数据集中标签的数量）的零张量，调用scatter_把 value=1 分配给索引对应的标签y上：

1	target_transform = Lambda(lambda y: torch.zeros(10,dtype=torch.float).scatter_(dim=0,index=torch.trnsor(y),value=1))

1.4 构建模型

构建神经网络

神经网络是由对数据进行处理的层/块组成。torch.nn命名空间提供了构建神经网络所需的构建块。pytorch中每个模型都是nn.Module的子类。神经网络本身就是由其他模块(层)组成的模块，这种嵌套结构可以轻松地构建和管理复杂的架构体系。

构建一个对FashionMNIST数据集中的图像进行分类的神经网络。

import os
import torch
from torch import nn
from torch.utils.data import DataLoader
from torchvision import datasets,transforms

获取训练资源：如果有cpu之类的硬件加速器，就在加速器上训练模型，查看torch.cuda是否可用，不可用则用cpu:

1 2	device = "cuda" if torch.cuda.is_available() else "cpu" print(device)

输出结果：

cuda

定义类：通过继承nn.Module来定义新的神经网络，并在__init__中初始化神经网络层。每一个nn.Module子类在forward方法中实现对输入数据的操作。

device = "cuda" if torch.cuda.is_available() else "cpu"
class NeuralNetwork(nn.Module):
    def __init__(self):
        super(NeuralNetwork,self).__init__()
        self.flatten = nn.Flatten()
        self.linear_relu_stack = nn.Sequential(
            nn.Linear(28*28,512),
            nn.ReLU(),
            nn.Linear(512,512),
            nn.ReLU(),
            nn.Linear(512,10)
        )

    def forward(self,x):
        x = self.flatten(x)
        logits = self.linear_relu_stack()
        return logits


model = NeuralNetwork().to(device)
print(model)

输出结果：

NeuralNetwork(
  (flatten): Flatten(start_dim=1, end_dim=-1)
  (linear_relu_stack): Sequential(
    (0): Linear(in_features=784, out_features=512, bias=True)
    (1): ReLU()
    (2): Linear(in_features=512, out_features=512, bias=True)
    (3): ReLU()
    (4): Linear(in_features=512, out_features=10, bias=True)
  )
)

将数据输入模型，这将执行模型的forward以及一些后台操作。不要直接调用model.forward()

在输入上调用模型将返回一个二维张量，其中 dim=0 对应于每个类的 10 个原始预测值的每个输出，dim=1 对应于每个输出的单个值。我们通过nn.Softmax模块的实例传递预测概率来获得预测概率。

Model Layers

在FashionMNIST模型中分解图层，小批量处理3张28*28的图片样本，观察通过网络时的样子：

1 2	input_image = torch.rand(3,28,28) print(input_image.size())

输出结果：

1	torch.Size([3, 28, 28])

nn.Flatten

flatten()是对多维数据的降维函数，默认缺省参数为0，也就是说flatten()和flatte(0)效果一样。python里的flatten(dim)表示，从第dim个维度开始展开，将后面的维度转化为一维.也就是说，只保留dim之前的维度，其他维度的数据全都挤在dim这一维。比如一个数据的维度是( S 0 , S 1 , S 2……… , S n ) (S0,S1,S2………,Sn)(S0,S1,S2………,Sn), flatten(m)后的数据为( S 0 ， S 1 ， S 2 ， . . . ， S m − 2 ， S m − 1 ， S m ∗ S m + 1 ∗ S m + 2 ∗ . . . ∗ S n ) (S0，S1，S2，…，Sm-2，Sm-1，SmSm+1Sm+2*…*Sn)(S0，S1，S2，…，Sm−2，Sm−1，Sm∗Sm+1∗Sm+2∗…∗Sn)

初始化 nn.Flatten图层，用来将每个 2D 28x28 图像转换为包含 784 个像素值的连续数组（（在 dim=0 时）保持小批量维度）。

1
2
3

flatten = nn.Flatten()
flat_image = flatten(input_image)
print(flat_image.size())

输出结果：

1 2	torch.Size([3, 28, 28]) torch.Size([3, 784])

nn.Linear

线性层是一个模块，它使用存储好的权重和偏差对输入进行线性转换。

1
2
3

layer1 = nn.Linear(in_features=28*28, out_features=20)
hidden1 = layer1(flat_image)
print(hidden1.size())

输出结果：

1	torch.Size([3, 20]) #表示列表中有3个元素，每个元素是一个新的列表，元素列表中有20个元素

nn.ReLU

非线性激活是在模型的输入和输出之间创建的复杂映射。它们应用于线性变换后引入非线性，帮助神经网络学习各种各样的现象。

此模型中，线性层之间使用nn.ReLU，非线性中引入其他激活量

1
2
3

print(f"Before ReLU: {hidden1}\n\n")
hidden1 = nn.ReLU()(hidden1)
print(f"After ReLU: {hidden1}")

输出结果：

Before ReLU: tensor([[ 0.1426, -0.3470, -0.1418, -0.3554, -0.1413, -0.1681, -0.1939, -0.0601,
          0.2604,  0.1082,  0.2209,  0.2681,  0.1723,  0.1945, -0.1162,  0.1421,
         -0.0883,  0.0151, -0.2167, -0.3203],
        [ 0.0153, -0.5945, -0.1802, -0.3600,  0.1283,  0.0200,  0.1102, -0.0895,
          0.3346,  0.1966,  0.2081,  0.1350,  0.4364,  0.3082,  0.1694, -0.1802,
         -0.5276,  0.3391,  0.2126, -0.1366],
        [ 0.0145, -0.2145, -0.4439, -0.1665, -0.1340,  0.0364, -0.5288, -0.1765,
          0.2297, -0.1475,  0.0147,  0.0021,  0.1454,  0.4573, -0.3557, -0.2232,
         -0.4160,  0.1634, -0.0264, -0.4376]], grad_fn=<AddmmBackward0>)


After ReLU: tensor([[0.1426, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.2604,
         0.1082, 0.2209, 0.2681, 0.1723, 0.1945, 0.0000, 0.1421, 0.0000, 0.0151,
         0.0000, 0.0000],
        [0.0153, 0.0000, 0.0000, 0.0000, 0.1283, 0.0200, 0.1102, 0.0000, 0.3346,
         0.1966, 0.2081, 0.1350, 0.4364, 0.3082, 0.1694, 0.0000, 0.0000, 0.3391,
         0.2126, 0.0000],
        [0.0145, 0.0000, 0.0000, 0.0000, 0.0000, 0.0364, 0.0000, 0.0000, 0.2297,
         0.0000, 0.0147, 0.0021, 0.1454, 0.4573, 0.0000, 0.0000, 0.0000, 0.1634,
         0.0000, 0.0000]], grad_fn=<ReluBackward0>)

进程已结束,退出代码0

nn.Sequential

nn.Sequential是模块的序列容器，数据按照定义的顺序传递给所有模块。可以使用序列容器把类似seq_modules的快速网络组合在一起。

seq_modules = nn.Sequential(
    flatten,
    layer1,
    nn.ReLU(),
    nn.Linear(20, 10)
)
input_image = torch.rand(3,28,28)
logits = seq_modules(input_image)
print('logits:','\n',logits)

输出结果：

logits: 
 tensor([[ 0.1616,  0.0817,  0.0735, -0.2260,  0.1975, -0.1653,  0.1895,  0.0527,
          0.0308, -0.0972],
        [ 0.1359,  0.1092,  0.1909, -0.1869,  0.3001, -0.1487,  0.2278,  0.1496,
         -0.0421, -0.0847],
        [ 0.1871,  0.0593,  0.1264, -0.1700,  0.3118, -0.2164,  0.1416,  0.1205,
         -0.0370, -0.0457]], grad_fn=<AddmmBackward0>)

nn.Softmax

神经网络的最后一个线性层返回logits 的原始值在区间[-infty, infty]内，这些值被传递给nn.Softmax模块。logits值被缩放在区间[0,1]内，表示模型对每个类的预测概率。Dim参数表示值之和为1的维度。

1
2
3

softmax = nn.Softmax(dim=1)
pred_probab = softmax(logits)
print('pred_probab:','\n',pred_probab)

输出结果：

pred_probab: 
 tensor([[0.1160, 0.0935, 0.1411, 0.0945, 0.1039, 0.0819, 0.1050, 0.0800, 0.0721,
         0.1120],
        [0.1140, 0.0928, 0.1494, 0.1022, 0.0992, 0.0822, 0.0972, 0.0789, 0.0727,
         0.1114],
        [0.1249, 0.0926, 0.1434, 0.0946, 0.1088, 0.0728, 0.0986, 0.0874, 0.0711,
         0.1058]], grad_fn=<SoftmaxBackward0>)

模型参数

神经网络中是许多层都是参数化的，即在训练过程中有相关的权重和偏差被优化。子类化nn.Module模块自动跟踪模型对象中定义的所有字段，并使用模型的parameters()或named_parameters()方法访问所有参数。

在这个例子中，我们迭代每个参数，并打印它的大小和预览其值。

1
2
3

print(f"Model structure: {model}\n\n")
for name, param in model.named_parameters():
    print(f"Layer: {name} | Size: {param.size()} | Values : {param[:2]} \n")

输出结果：

Model structure: NeuralNetwork(
  (flatten): Flatten(start_dim=1, end_dim=-1)
  (linear_relu_stack): Sequential(
    (0): Linear(in_features=784, out_features=512, bias=True)
    (1): ReLU()
    (2): Linear(in_features=512, out_features=512, bias=True)
    (3): ReLU()
    (4): Linear(in_features=512, out_features=10, bias=True)
  )
)


Layer: linear_relu_stack.0.weight | Size: torch.Size([512, 784]) | Values : tensor([[-0.0185,  0.0094, -0.0099,  ...,  0.0073,  0.0120, -0.0207],
        [ 0.0332,  0.0094,  0.0302,  ..., -0.0288, -0.0147, -0.0188]],
       device='cuda:0', grad_fn=<SliceBackward0>) 

Layer: linear_relu_stack.0.bias | Size: torch.Size([512]) | Values : tensor([0.0175, 0.0353], device='cuda:0', grad_fn=<SliceBackward0>) 

Layer: linear_relu_stack.2.weight | Size: torch.Size([512, 512]) | Values : tensor([[ 0.0042, -0.0256, -0.0213,  ..., -0.0243,  0.0143,  0.0336],
        [-0.0410,  0.0155, -0.0331,  ..., -0.0383,  0.0384,  0.0250]],
       device='cuda:0', grad_fn=<SliceBackward0>) 

Layer: linear_relu_stack.2.bias | Size: torch.Size([512]) | Values : tensor([-0.0219,  0.0169], device='cuda:0', grad_fn=<SliceBackward0>) 

Layer: linear_relu_stack.4.weight | Size: torch.Size([10, 512]) | Values : tensor([[-0.0372, -0.0264,  0.0106,  ...,  0.0389,  0.0076,  0.0132],
        [ 0.0309,  0.0214,  0.0044,  ..., -0.0207, -0.0020, -0.0263]],
       device='cuda:0', grad_fn=<SliceBackward0>) 

Layer: linear_relu_stack.4.bias | Size: torch.Size([10]) | Values : tensor([-0.0196,  0.0350], device='cuda:0', grad_fn=<SliceBackward0>)

1.5 自动求导Autograd

在训练神经网络时，最常用的算法是反向传播。在该算法中，参数(模型权重)根据损失函数相对于给定参数的梯度进行调整。为了计算这些梯度，PyTorch内置了一个名为torch.autograd的微分引擎。它支持自动计算任何计算图的梯度。

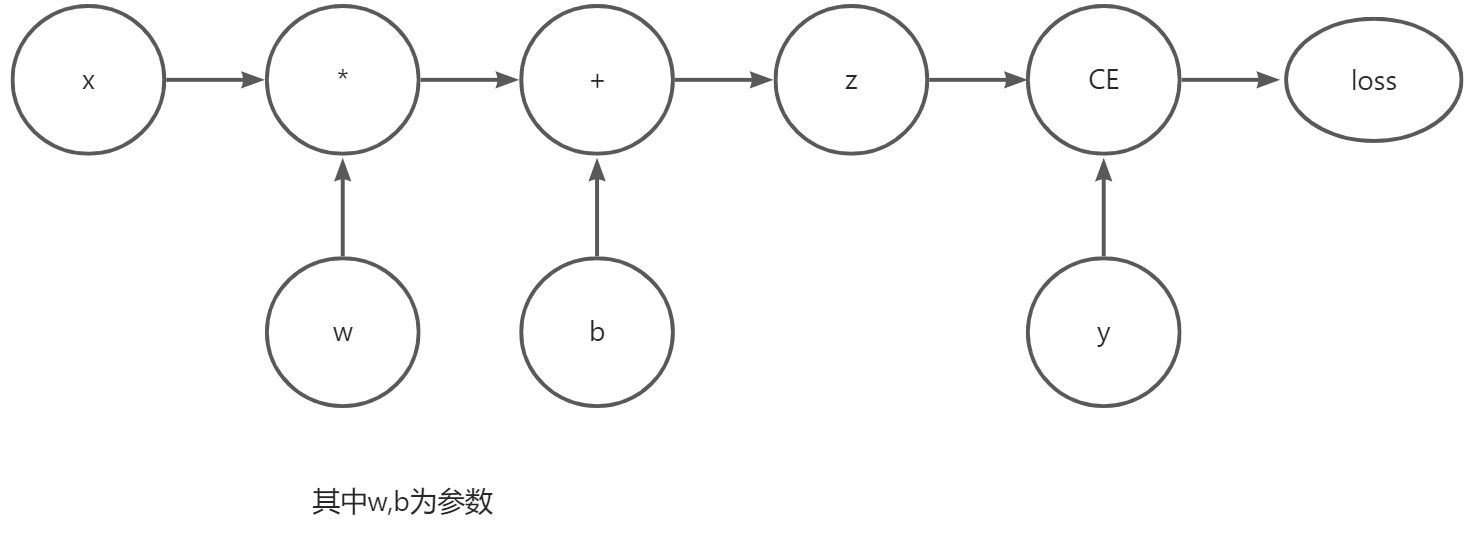
考虑最简单的单层神经网络，输入x，参数w和b，以及一些损失函数。它可以在PyTorch中以如下方式定义：

import torch

x = torch.ones(5) #input tensor
y = torch.zeros(3) #expected output
w = torch.randn(5,3,requires_grad=True)
b = torch.randn(3,requires_grad=True)
z = torch.matmul(x,w)+b
loss = torch.nn.functional.binary_cross_entropy_with_logits(z,y)

Tensors, Functions and Computational graph

这段代码定义了以下计算图：

在这个网络中，优化参数w和b，需要计算损失函数的梯度，为了做到这一点，我们设置这些张量的requires_grad属性。

1	您可以在创建张量时设置requires_grad的值，或者稍后使用x.requires_grad_(True)方法。

应用在张量上构造计算图的函数实际上是一个函数类的对象。该对象知道如何在正方向计算函数，也知道在反向传播过程中如何计算其导数。反向传播函数的引用存储在张量的grad_fn属性中，更多信息请参考function文档。

1 2	print(f"Gradient function for z = {z.grad_fn}") print(f"Gradient funxtion for loss = {loss.grad_fn}")

输出结果：

1 2	Gradient function for z = <AddBackward0 object at 0x000001FA3EAB56D0> Gradient funxtion for loss = <BinaryCrossEntropyWithLogitsBackward0 object at 0x000001FA3EAB56D0>

梯度计算

优化神经网络参数的权重，需要计算损失函数对参数的导数，即计算固定x和y值的和，调用loss.backward()来计算这些导数，然后从w.grad 和 b.grad检索值：

1
2
3

loss.backward()
print(w.grad)
print(b.grad)

输出结果：

tensor([[0.0405, 0.0236, 0.1284],
        [0.0405, 0.0236, 0.1284],
        [0.0405, 0.0236, 0.1284],
        [0.0405, 0.0236, 0.1284],
        [0.0405, 0.0236, 0.1284]])
tensor([0.0405, 0.0236, 0.1284])

1
2
3

1.只能获取计算图的叶节点的grad属性，它们的requires_grad属性设置为True，图中的其他节点找不到梯度。

2.由于性能原因，只能在给定的图上使用一次向后梯度计算。如果需要对同一个图进行几个向后调用，则需要将retain_graph=True传递给向后调用。

禁用梯度跟踪Disabling Gradient Tracking

默认情况下，所有require_grad =True的张量都会跟踪其计算历史，支持梯度计算。但是，在某些情况下不需要这样做。例如，训练的模型只是想把它应用到一些输入数据上，即只想通过网络进行正向计算。通过使用torch.no_grad()块包围需要计算的代码来停止跟踪计算：

z = torch.matmul(x,w)+b
print(z.requires_grad)

with torch.no_grad():
    z = torch.matmul(x,w)+b
print(z.requires_grad)

输出结果：

1 2	True False

另一种实现相同结果的方法是对张量使用detach()方法:

1
2
3

z = torch.matmul(x,w)+b
z_det = z.detach()
print(z_det.requires_grad)

输出结果：

False

禁用梯度跟踪的原因如下：

将神经网络中的一些参数标记为冻结参数，这是一个微调预训练网络的常见方案；
在只向正向传递时加快计算速度，因为在不跟踪梯度张量上的计算将更加高效。

有关计算图的更多信息

从概念上讲，autograd 在由 Function 对象组成的有向无环图(DAG)中保留数据(张量)和所有已执行操作(以及生成的新张量)的记录。在此 DAG 中，叶子是输入张量，根是输出张量。通过从根到叶跟踪此图，可以使用链式规则自动计算梯度。

在正向传递中，autograd同时执行两项操作：

运行请求操作来计算产生的张量** ；**
在 DAG 中维护运算的梯度函数。

当在DAG root. autograd上调用.backward()时，向后传递开始，然后:

计算每个.grad_fn的梯度；
将它们累积在相应张量的.grad属性中；
使用链规则，一直传播到叶张量。

在PyTorch中，DAG是动态的。在每次.backward()调用之后，autograd开始填充一个新的图。这正是允许在模型中使用控制流语句的原因;如果需要，可以在每次迭代中更改形状、大小和操作。

选读：张量梯度和雅可比积

在许多情况下，我们有一个标量损失函数，我们需要计算相对于某些参数的梯度。但是，在某些情况下，输出函数是任意张量。在这种情况下，PyTorch 允许计算所谓的雅可比积，而不是实际的梯度。

向量函数,其中,。对的梯度由雅可比矩阵给出:

对于给定的输入向量， PyTorch允许计算雅可比矩阵，而不是计算雅可比矩阵本身。这是通过反向调用作为参数来实现的,的大小应该和原始张量的大小相同，我们要根据它来计算乘积:

inp = torch.eye(4,5,requires_grad=True)
out = (inp+1).pow(2).t()  #pow()幂函数，t()转置
out.backward(torch.ones_like(out),retain_graph=True)
print(f"First call \n {inp.grad}")
out.backward(torch.ones_like(out),retain_graph=True)
print(f"\nSensond call \n {inp.grad}")
out.backward(torch.ones_like(out),retain_graph=True)
print(f"\n Call after zeroing gradient \n {inp.grad}")

其中，torch.eye()函数主要是为了生成对角线全为1，其余部分全为0的二维数组；

函数原型： torch.eye(n，m=None，out=None)；
参数解释：n行数，m列数，out输出类型。

输出结果：

First call 
 tensor([[4., 2., 2., 2., 2.],
        [2., 4., 2., 2., 2.],
        [2., 2., 4., 2., 2.],
        [2., 2., 2., 4., 2.]])

Sensond call 
 tensor([[8., 4., 4., 4., 4.],
        [4., 8., 4., 4., 4.],
        [4., 4., 8., 4., 4.],
        [4., 4., 4., 8., 4.]])

 Call after zeroing gradient 
 tensor([[12.,  6.,  6.,  6.,  6.],
        [ 6., 12.,  6.,  6.,  6.],
        [ 6.,  6., 12.,  6.,  6.],
        [ 6.,  6.,  6., 12.,  6.]])

注意，当使用相同的参数第二次向后调用时，梯度的值是不同的。这是因为在做反向传播时，PyTorch会对梯度进行累加，即计算出的梯度的值被添加到计算图的所有叶子节点的grad属性中。如果想计算正确的梯度，需要在此之前将grad属性归零。在现实训练中，优化器可以帮助我们做到这一点。

以前调用的backward()函数不带参数，这本质上相当于向后调用(torch.tensor(1.0))，对于标量值函数是一种计算梯度的有效方法，如神经网络训练期间的损耗。

1.6 优化Optimization

优化模型参数

现在我们有了一个模型和数据，通过在数据上优化其参数来训练、验证和测试模型。训练一个模型是一个迭代的过程；在每次迭代(称为epoch)中，模型对输出进行猜测，计算猜测中的误差(损失)，收集误差对其参数的导数(正如我们在前一节中看到的)，并使用梯度下降优化这些参数。关于这个过程的更详细的演练，请查看来自backpropagation from 3Blue1Brown。

前提代码

我们将从前面的章节数据集和数据载入器以及构建模型中加载部分代码。

import torch
from torch import nn
from torch.utils.data import DataLoader
from torchvision import datasets
from torchvision.transforms import ToTensor


training_data = datasets.FashionMNIST(
    root='data',
    train=True,
    download=True,
    transform=ToTensor()
)

test_data = datasets.FashionMNIST(
    root='data',
    train=True,
    download=True,
    transform=ToTensor()
)

train_dataloader = DataLoader(training_data,batch_size=64)
test_dataloader = DataLoader(training_data,batch_size=64)

class NeuralNetwork(nn.Module):
    def __init__(self):
        super(NeuralNetwork,self).__init__()
        self.flatten = nn.Flatten()
        self.linear_relu_stack = nn.Sequential(
            nn.Linear(28*28,512),
            nn.ReLU(),
            nn.Linear(512,512),
            nn.ReLU(),
            nn.Linear(512,10),
        )

    def forward(self,x):
        x = self.flatten(x)
        logits = self.linear_relu_stack(x)
        return logits

model = NeuralNetwork()
print(model)

输出结果：

NeuralNetwork(
  (flatten): Flatten(start_dim=1, end_dim=-1)
  (linear_relu_stack): Sequential(
    (0): Linear(in_features=784, out_features=512, bias=True)
    (1): ReLU()
    (2): Linear(in_features=512, out_features=512, bias=True)
    (3): ReLU()
    (4): Linear(in_features=512, out_features=10, bias=True)
  )
)

超参数

超参数是可调整的参数，可用于控制模型优化过程。不同的超参数值会影响模型训练和收敛速率（阅读更多有关超参数优化信息）。

为训练定义以下超参数：

纪元(epoch)数量 - 在数据上迭代的次数；
批量大小 - 在更新参数之前通过网络传播的数据样本数；
学习率 - 每个批次/epoch更新模型参数的多少。较小的值会导致学习速度较慢，而较大的值可能会导致训练期间不可预测的行为。
1
2
3
learning_rate = 1e-3
batch_size = 64
epochs = 5

优化循环

设置了超参数，可以使用优化循环来训练和优化模型，优化循环的每次迭代称为一个纪元(epoch)。每个纪元由两部分组成：

训练循环 - 遍历训练数据集，试图收敛到最优参数。
验证/测试循环-对测试数据集进行迭代，以检查模型性能是否正在改善。

地熟悉一下训练循环中使用的一些概念，跳到前面，查看优化循环的Full Implementation。

损失函数

当面对一些训练数据时，我们未经训练的网络很可能不会给出正确的答案。损失函数衡量所获得的结果与目标值的相似程度，是在训练过程中想要最小化的损失函数。为了计算损失，我们使用输入的数据样本进行预测，并将其与真实的数据标签值进行比较。

常用的损失函数包括nn.MSELoss(均方差)用于回归；nn.NLLLoss(负对数似然)用于分类。nn.CrossEntropyLoss结合了nn.LogSoftmax 和 nn.NLLLoss。

将模型的输出对数传递给nn.CrossEntropyLoss，将对数归一化并计算预测误差。

1	loss_fn = nn.CrossEntropyLoss()

优化器

优化是调整模型参数以减少每个训练步骤中的模型误差的过程。优化算法定义了如何执行此过程(在此示例中，使用随机梯度下降法)。所有优化逻辑都封装在优化器对象中，这里使用SGD优化器；此外，PyTorch中还有许多优化器，比如ADAM和RMSProp，它们可以更好地处理不同类型的模型和数据。

通过自动记录需要训练的模型参数，并传入学习速率超参数来初始化优化器。

1	optimizer = torch.optim.SGD(model.parameters(),lr=learning_rate)

在训练循环中，优化分为三个步骤：

调用optimizer.zero_grad()重置模型参数的梯度。梯度默认情况下是叠加的；为了防止重复计算，在每次迭代时将它们归零。
通过调用loss.backward()反向传播预测损失。PyTorch保存每个参数的损耗w.r.t.的梯度。
有了梯度，调用optimizer.step()来通过反向传递中收集的梯度来调整参数。

全面实施

在优化代码上定义循环train_loop，并根据测试数据评估模型性能。

def train_loop(dataloader,model,loss_fn,opimiizer):
    size = len(dataloader.dataset)
    for batch, (X,y) in enumerate(dataloader):
        #计算预测和损失compute prediction and loss
        pred = model(X)
        loss = loss_fn(pred,y)

        #反向传播Backpropagetion
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        if batch % 100 == 0:
            loss ,current = loss.item(), batch * len(X)
            print(f"loss: {loss:>7f} [{current:>5d}/{size:>5d}]")


def mytest_loop(dataloader,model,loss_fn):
    size = len(dataloader.dataset)
    num_batches = len(dataloader)
    test_loss,correct = 0,0
    with torch.no_grad():
        for X,y in dataloader:
            pred = model(X)
            test_loss += loss_fn(pred, y).item()
            correct += (pred.argmax(1) == y).type(torch.float).sum().item()
    test_loss /= num_batches
    correct /= size
    print(f"Test Error: \n Accuracy: {(100*correct):>0.1f}%, Avg loss: {test_loss:>8f} \n")

初始化损失函数和优化器，并将其传递给train_loop和test_loop。还可以随意增加epoch的数量，以跟踪模型的改进性能。

loss_fn = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(),lr=learning_rate)

epochs = 10
for t in range(epochs):
    print(f"Epoch {t+1}\n------------------------------------")
    train_loop(train_dataloader,model,loss_fn,optimizer)
    mytest_loop(test_dataloader,model,loss_fn)
print("Done!")

整体输出结果：

Epoch 1
------------------------------------
loss: 2.298616 [    0/60000]
loss: 2.286485 [ 6400/60000]
loss: 2.270025 [12800/60000]
loss: 2.269643 [19200/60000]
loss: 2.253848 [25600/60000]
loss: 2.225894 [32000/60000]
loss: 2.233021 [38400/60000]
loss: 2.200334 [44800/60000]
loss: 2.193990 [51200/60000]
loss: 2.175176 [57600/60000]
Test Error: 
 Accuracy: 55.8%, Avg loss: 2.162668 

Epoch 2
------------------------------------
loss: 2.167829 [    0/60000]
loss: 2.157712 [ 6400/60000]
loss: 2.098750 [12800/60000]
loss: 2.122153 [19200/60000]
loss: 2.079582 [25600/60000]
loss: 2.016336 [32000/60000]
loss: 2.051298 [38400/60000]
loss: 1.968452 [44800/60000]
loss: 1.977741 [51200/60000]
loss: 1.917104 [57600/60000]
Test Error: 
 Accuracy: 58.1%, Avg loss: 1.903896 

Epoch 3
------------------------------------
loss: 1.933278 [    0/60000]
loss: 1.899875 [ 6400/60000]
loss: 1.783205 [12800/60000]
loss: 1.834392 [19200/60000]
loss: 1.734482 [25600/60000]
loss: 1.675408 [32000/60000]
loss: 1.713700 [38400/60000]
loss: 1.606300 [44800/60000]
loss: 1.643087 [51200/60000]
loss: 1.542788 [57600/60000]
Test Error: 
 Accuracy: 62.6%, Avg loss: 1.543185 

Epoch 4
------------------------------------
loss: 1.609218 [    0/60000]
loss: 1.570532 [ 6400/60000]
loss: 1.422559 [12800/60000]
loss: 1.495395 [19200/60000]
loss: 1.385326 [25600/60000]
loss: 1.368906 [32000/60000]
loss: 1.391647 [38400/60000]
loss: 1.310771 [44800/60000]
loss: 1.353835 [51200/60000]
loss: 1.252852 [57600/60000]
Test Error: 
 Accuracy: 64.8%, Avg loss: 1.263495 

Epoch 5
------------------------------------
loss: 1.341740 [    0/60000]
loss: 1.325438 [ 6400/60000]
loss: 1.159720 [12800/60000]
loss: 1.261750 [19200/60000]
loss: 1.144259 [25600/60000]
loss: 1.157326 [32000/60000]
loss: 1.183641 [38400/60000]
loss: 1.119133 [44800/60000]
loss: 1.165480 [51200/60000]
loss: 1.080092 [57600/60000]
Test Error: 
 Accuracy: 66.2%, Avg loss: 1.084698 

Epoch 6
------------------------------------
loss: 1.155534 [    0/60000]
loss: 1.166295 [ 6400/60000]
loss: 0.982190 [12800/60000]
loss: 1.115493 [19200/60000]
loss: 0.992656 [25600/60000]
loss: 1.013594 [32000/60000]
loss: 1.055350 [38400/60000]
loss: 0.997410 [44800/60000]
loss: 1.044053 [51200/60000]
loss: 0.973711 [57600/60000]
Test Error: 
 Accuracy: 67.4%, Avg loss: 0.970132 

Epoch 7
------------------------------------
loss: 1.027112 [    0/60000]
loss: 1.064346 [ 6400/60000]
loss: 0.861960 [12800/60000]
loss: 1.019788 [19200/60000]
loss: 0.897487 [25600/60000]
loss: 0.914093 [32000/60000]
loss: 0.973150 [38400/60000]
loss: 0.919831 [44800/60000]
loss: 0.962260 [51200/60000]
loss: 0.904603 [57600/60000]
Test Error: 
 Accuracy: 68.6%, Avg loss: 0.893350 

Epoch 8
------------------------------------
loss: 0.934642 [    0/60000]
loss: 0.994998 [ 6400/60000]
loss: 0.776983 [12800/60000]
loss: 0.953107 [19200/60000]
loss: 0.834409 [25600/60000]
loss: 0.842692 [32000/60000]
loss: 0.916326 [38400/60000]
loss: 0.868921 [44800/60000]
loss: 0.904816 [51200/60000]
loss: 0.856013 [57600/60000]
Test Error: 
 Accuracy: 69.8%, Avg loss: 0.838920 

Epoch 9
------------------------------------
loss: 0.865317 [    0/60000]
loss: 0.943758 [ 6400/60000]
loss: 0.714329 [12800/60000]
loss: 0.903987 [19200/60000]
loss: 0.789997 [25600/60000]
loss: 0.789787 [32000/60000]
loss: 0.874063 [38400/60000]
loss: 0.833949 [44800/60000]
loss: 0.862678 [51200/60000]
loss: 0.819333 [57600/60000]
Test Error: 
 Accuracy: 71.0%, Avg loss: 0.798254 

Epoch 10
------------------------------------
loss: 0.811143 [    0/60000]
loss: 0.902883 [ 6400/60000]
loss: 0.666282 [12800/60000]
loss: 0.866518 [19200/60000]
loss: 0.756904 [25600/60000]
loss: 0.749717 [32000/60000]
loss: 0.840520 [38400/60000]
loss: 0.808478 [44800/60000]
loss: 0.830349 [51200/60000]
loss: 0.790129 [57600/60000]
Test Error: 
 Accuracy: 72.3%, Avg loss: 0.766204 

Done!

1.7 保存&加载模型

保存并加载模型

本节介绍如何通过保存、加载、运行模型预测来保持模型状态。

1 2	import torch import torchvision.models as models

保存和加载模型权重

PyTorch模型将学习到的参数存储在一个名为state_dict的内部状态字典中，这些可以通过torch.save方法持久化:

1 2	model = models.vgg16(pretrained=True) torch.save(model.state_dict(),'model_weights.pth')

输出结果：

C:\ProgramData\Anaconda3\lib\site-packages\torchvision\models\_utils.py:208: UserWarning: The parameter 'pretrained' is deprecated since 0.13 and will be removed in 0.15, please use 'weights' instead.
  warnings.warn(
C:\ProgramData\Anaconda3\lib\site-packages\torchvision\models\_utils.py:223: UserWarning: Arguments other than a weight enum or `None` for 'weights' are deprecated since 0.13 and will be removed in 0.15. The current behavior is equivalent to passing `weights=VGG16_Weights.IMAGENET1K_V1`. You can also use `weights=VGG16_Weights.DEFAULT` to get the most up-to-date weights.
  warnings.warn(msg)
Downloading: "https://download.pytorch.org/models/vgg16-397923af.pth" to C:\Users\sy/.cache\torch\hub\checkpoints\vgg16-397923af.pth
100%|██████████| 528M/528M [00:28<00:00, 19.2MB/s]

要加载模型权重，需要先创建同一个模型的实例，然后使用load_state_dict()方法加载参数。

1
2
3

model = models.vgg16()    #不指定pretrained=True,是不加载默认权重
model.load_state_dict(torch.load('model_weights.pth'))
model.eval()

1	请务必在推理之前调用方法model.eval()，以将丢弃层和批处理归一化层设置为评估模式。如果不这样做，将产生不一致的推理结果。

Saving and Loading Models with Shapes

加载模型权重时，需要先实例化模型类，因为该类定义了网络的结构。如果将此类的结构与模型一起保存，在这种情况下，可以将model (而不是model.state_dict()) 传递给save函数：

1	torch.save(model,'model.pth')

然后可以这样加载模型:

1	model = torch.load('model.pth')

延伸阅读

Saving and Loading a General Checkpoint in PyTorch

0 预备

Anaconda安装

conda进入base基本环境

conda退出base环境及其常用命令

管理员windows powershell进入base环境

取消打开管理员就进入conda base环境的方法：

sudo安装

pycharm配置设置

pycharm中删除已有的python解析器：

python面向对象

类定义

类对象和__init__

self代表类的实例，而非类

类的方法

继承

多继承

方法重写

类属性与方法

类的专有方法：

运算符重载

Matplotlib

matplotlib安装

Matplotlib Pyplot

Matplotlib绘图标记

fmt参数

Matplotlib绘图线

线的类型

线的颜色

安装pytorch

检查是否有合适的GPU

安装pytorch

1 pytorch简介

1.1 张量

初始化张量

直接从数据中创建

从Numpy数组中创建

从其他张量创建

随机或常量值

张量属性

张量运算

标准化的numpy类索引和切片

Arithmetic operations算数运算

Single-element tensors单元张量

In-place operations就地操作

Bridge with NumPy

1.2 数据集和数据加载器

数据集加载

迭代和可视化数据集

自定义数据集

init

len

getitem

用数据加载器数据进行训练

循环访问数据加载器

延伸阅读

1.3 Transform

ToTensor

Lambda Transforms

延伸阅读

1.4 构建模型

构建神经网络

Model Layers

nn.Flatten

nn.Linear

nn.ReLU

nn.Sequential

nn.Softmax

模型参数

延伸阅读

1.5 自动求导Autograd

Tensors, Functions and Computational graph

梯度计算

禁用梯度跟踪Disabling Gradient Tracking

有关计算图的更多信息

选读：张量梯度和雅可比积

延伸阅读

1.6 优化Optimization

优化模型参数

前提代码

超参数

类对象和init