自动摘要: 原文链接:[ImplicitFunctionLearning](https://www.hummat.com/learning/2022/02/23/implicitfunctionlearn ……..
原文链接:Implicit Function Learning正如标题所暗示的那样,本文涉及两个主题:
- 什么是隐式函数?
- 如何从任意形状的数据中学习它们?
当然,我们从第一个开始。
什么是隐式函数?
您可能熟悉数学和编程中的函数概念。两者的共同点是,您提供一个或多个输入并获得一个或多个输出
,如
。由于我们想在 3D 形状表示的上下文中了解函数,因此请考虑描述以原点为中心的球体表面的函数
其中
和
是方位角和极角,
且角度为
的球体,我们得到 。

这是定义函数的 _显式 _或 _参数_化 方法:给定球体半径,我们可以直接计算其表面上任意球面坐标
的所有点坐标,作为
。下面是定义函数的方式:给定球体半径,我们可以直接计算其表面上任意球面坐标的所有点坐标定义的相同函数:
这个方程提供了从任何点到球体表面的平方距离
)。在此过程中,我们隐式地将球体表面定义为所谓的这是隐式函数的标准形式。方程返回零的所有点都位于球体表面(定义为所谓的“零水平集”(“zero-level set”))。此外,我们知道所有点,即距离为零的 ISO 表面,在高程或ISO
的上下文中您可能熟悉这个概念1在拓扑图上。
为什么它们有用?
请记住开头介绍的简单但强大的方程,该方程描述了球体表面上_具有_任意半径的所有点。现在尝试为以下形状找到类似的公式2:
是的,我也不是。不过,我们仍然可以相当有效地计算每个点,无论它位于形状内部还是外部。为此,我们在远处选择第二个肯定不在形状内的点,并将其与我们的兴趣点连接起来3. 然后我们执行三角形交集测试(因为我们确实有一个形状的三角形网格)。对于每个三角形,我们首先无限扩展它以形成一个平面,并计算我们的线(或射线)与它的交点(前提是直线和平面不垂直,我们可以通过计算平面法线向量和直线的点积来检查)。如果平面和直线相交,我们检查交点是否位于所有三角形边的左侧。如果是这样,则三角形和直线相交4.现在,偶数个交叉点意味着兴趣点位于形状之外(我们已经进入和退出),而不偶数意味着我们在内部。

多次重复此过程可将空间(例如
立方体)分为外部(多次重复此过程可提供空间的分离,例如)、分为外部(红色)、内部(蓝色)和中间(白色),其中中间隐含地将形状的表面描述为既不在形状内部也不在形状外部的空间。
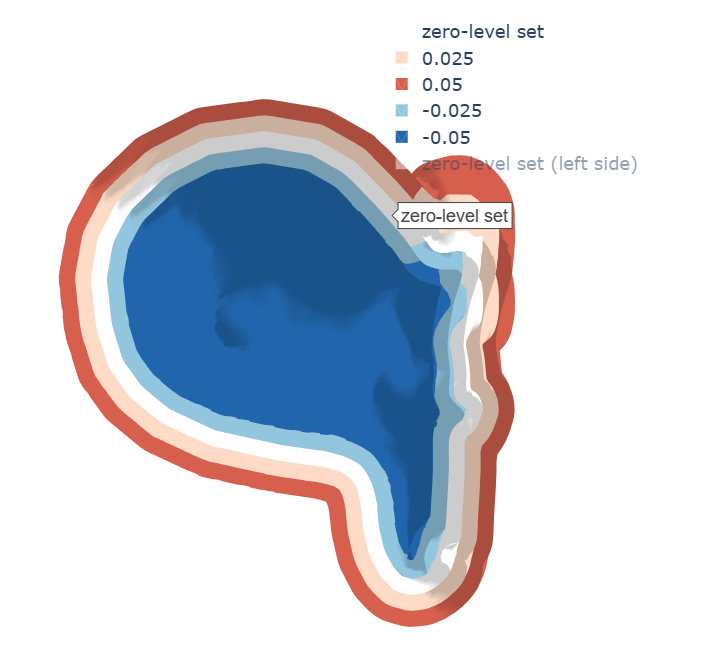
除了计算兴趣点是否在形状外部,我们还可以计算其距离,其中正距离表示外部,负内部表示,如之前的球体示例5.这对于一般形状的计算要复杂一些,并且通常没有必要,我们将在后面看到。下面您可以看到零水平集表面以及周围水平的横截面。
如何学习它们?
在我们深入研究这个问题之前,让我们先快速介绍另一个问题:为什么?如果您以前处理过3D数据(在深度学习或其他方面),您可能知道有很多方法可以表示它,这与图像不同,图像的绝对标准是像素网格。

每种表示形式都有其优点和缺点。虽然点云是轻量级的,但由于它们的混乱,它们很难处理。另一方面,体素网格很容易通过卷积等标准操作进行处理,但在细节损失和大尺寸之间需要权衡。网格最终是一种有效的表示形式,对下游任务具有很好的属性,但非常难以学习,因为需要跟踪顶点和三角形及其相互依赖性6.
我们想要的是一种富有表现力、低成本(计算和存储方面的智能)且易于学习的表示。好吧,您可能已经看到了这是怎么回事,但是隐式函数是如何组合所有这些宏伟属性的呢?
让我们从最后开始:它们很容易学习,因为它们定义了一个简单的学习任务。学习一个点是位于内部还是外部可以很容易地转换为二元分类问题(请参阅上图中的_概率_选项卡)。在我们的例子中,该模型是一个深度神经网络,它学习为我们预定义的体积(
立方体)中的每个点分配一个分数(又名logit)。当通过 sigmoid 函数并解释为概率时,对象的表面由两个类之间的决策边界隐式定义,即概率为 0.5 。
另一方面,学习预测到表面的符号距离是一种经典的回归设置。我们可以简单地学习最小化每个点的实际标量距离值和预测标量距离值之间的差异。
现在,为了了解其他两个理想的属性,让我们看一下旨在学习二进制占用值的网络体系结构:占用网络。
占用网络

https://avg.is.mpg.de/publications/occupancy-networks
从左到右:我们决定输入数据表示。根据它,我们使用从标准操作(如 2D 或 3D 卷积、全连接层、残差连接等)构建的编码器。例如,在处理图像时,我们可以使用在ImageNet上预先训练的ResNet主干(卷积部分),或者在输入由点集(点云)组成时使用PointNet,即投影深度图或LiDAR扫描。
输出是描述输入的_全局_特征向量。现在有趣的部分来了。我们使用由多个全连接层(_多层感知_器或MLP)组成的解码器,交出全局特征向量并要求它预测任意(随机采样)连续点位置,以预测它们的二进制占用概率。输入定义的形状内部接近 概率为1 ,外部接近 概率为0 。对训练数据集中的所有形状进行多次操作,MLP 学习,或者更确切地说,成为基于输入的空间划分,即空置和占用空间的三维概率分布。
这是隐式表示的表现力和效率的关键,因为(小)MLP可以以连续的方式编码数百个形状表面,即任意分辨率。
不过有一个问题。由于特征向量全局描述输入,因此输入、特征和输出空间之间没有空间对应关系,因此生成的形状缺乏细节并且过于平滑。幸运的是,这是可以解决的。
卷积占用网络

https://is.mpg.de/publications/peng2020eccv
通过将输入空间划分为体素,可以构建离散的特征网格,允许在空间上将输入和输出与特征空间相关联。由于网格网分辨率有限,因此连续点位置与来自 3D UNet 的修复要素进行匹配并进行三线性插值。解码器保持不变,但馈送具有更高质量的特征,从而产生具有更高频率信息的详细形状。
隐式特征网络

隐式特征网络https://virtualhumans.mpi-inf.mpg.de/ifnets
最后,在_隐式_特征网络中实现了类似的想法,但编码器使用3D特征金字塔提取多尺度特征,而不是在解码器端进行特征修复和插值,类似于检测和分割网络中已知的2D pendant 。
提取网格
现在,您可能想知道如何从隐式表示中实际获取网格。在训练期间,我们要求模型预测随机点位置的占用率,而在推理过程中,我们改为以任意分辨率提取规则网格上的占用率。获得每个体素被占用或未被占用(或填充有占用概率或有符号距离值)的网格后,我们可以使用经典的_行进立方体_方法来提取网格。
有什么问题吗?
是的。虽然大多数工作都集中在像ShapeNet这样的基准数据上,但现实世界更加混乱。形状完成的一个有前途的应用是机器人操作,但从RGB-D相机获得的数据并不理想。数据是嘈杂的,由于过度反射的材料而缺少零件,没有典型的姿势 - 由于机器人相对于物体的位置和物体在世界中的姿势 - 当然还有非常不同的形状和大小。
让我们看看一些结果!
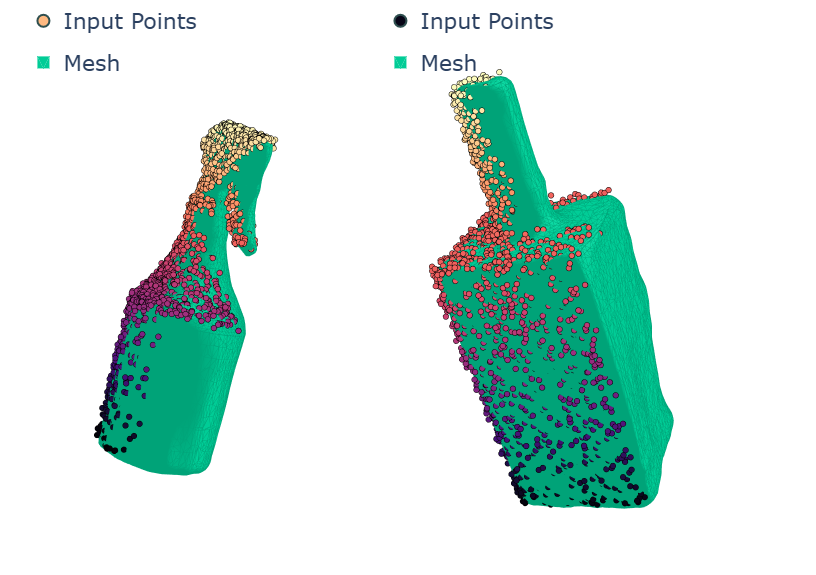
下面是通过投影深度图像获得的输入点云的一些可视化效果,以及它们以提取网格的形式完成,您可以通过单击每个图例中的网格来混合这些_网格_。
可以看出,该网络能够完成一组相当多样化的形状,尽管它们都来自同一类(瓶子)。今天就讲到这里。像往常一样,可以在下面找到用于生成可视化的代码。请注意,这次用于生成数字的数据太大,因此我不会将其包含在存储库中。
代码和参考
| Code法典 | [
](https://mybinder.org/v2/gh/hummat/hummat.github.io/master?labpath=notebooks%2Fimplicit-function-learning.ipynb) |
| — | — |
| [1] | Mescheder et al.: Occupancy Networks: Learning 3D Reconstruction in Function Space |
| [2] | Peng et al.: Convolutional Occupancy NetworksPeng et al.: 卷积占用网络 |
| [3] | Chibane et al.: Implicit Functions in Feature Space for 3D Shape Reconstruction and Completion |
- A curve along which a continuous field has a constant value. ↩连续场沿其具有常量值的曲线。↩
- Introducing Suzanne, the mascot of the awesome open source 3D software Blender. ↩介绍Suzanne,令人敬畏的开源3D软件Blender的吉祥物。↩
- This is sometimes called “shooting a ray from an arbitrary viewpoint”. ↩这有时被称为“从任意角度拍摄光线”。↩
- Check out this site if you are curious and want more details. ↩如果您好奇并想了解更多详细信息,请查看此网站。↩
- By hovering over a point you can see its distance to the surface. ↩通过将鼠标悬停在一个点上,您可以看到它与表面的距离。↩
- You can read more on each representation in my previous posts on learning from point clouds, voxel grids, graphs and meshes or projections. ↩您可以在我之前关于从点云、体素网格、图形和网格或投影中学习的文章中阅读有关每种表示的更多信













