自动摘要: 链接: [What’stheSituationwithIntelligentMeshGeneration:ASurveyandPerspectives](https://ar ……..

链接:

What’s the Situation with Intelligent Mesh Generation: A Survey and Perspectives

GitHub - xzb030/IMG_Survey

引言

动机

在本文中，我们开始对以智能网格生成（IMG）为中心的出版物进行系统回顾。网格生成被公认为美国宇航局“愿景 2030”[1] 的六个基础研究方向之一，在计算几何中起着举足轻重的作用，是数值模拟不可或缺的一部分。IMG 将机器学习与网格生成相结合，其重要性正在得到认可，因为它是一个不断增长的研究语料库，探索使用神经网络在不同的应用场景中生成高质量的网格。在各种网格划分目标的推动下，IMG 研究的兴趣激增。值得注意的是，近年来出现了许多创新算法。尽管对 IMG 进行了大量研究，但明显缺乏采用标准化方法以确保重要性、完整性和公正性的综合综述。为了推进 IMG 领域的研究，迫切需要对当前最先进的 IMG 方法进行系统概述。这样的概述将有助于提炼这些作品的基本共性，确定当前的研究趋势，并确定有希望的未来方向。在这里，我们的目标是提出一个全面和系统的调查，包括详细的分类和以内容为导向的评估。我们进行了多方面的分析，研究了关键算法技术及其应用范围、智能体学习目标、数据类型、有针对性的挑战，以及优势和局限性。如图所示。1、我们为现有的 IMG 方法提供了不同的分类法，从三个角度进行概念化：关键技术、输出网格单元元素和相关数据类型。考虑到关键技术，我们将 IMG 方法分为基于变形的、基于分类的、基于等值面的、基于 Delaunay 三角测量的、基于参数化的和基于前沿的网格生成。从输出网格单元单元的角度来看，IMG 方法分为三角网格、四边形网格、混合多边形网格和四面体网格生成。最后，我们将应用程序输入数据类型分为基于点云、基于图像、基于体素、基于网格、基于边界或草图以及基于潜在变量的网格生成。此外，我们还简要概述了 IMG 的相关领域，例如用于网格学习的传统神经网络、网格质量指标和数据集。综上所述，我们研究和审查了 190 篇论文，其中包括 113 篇关注 IMG 的论文和 77 篇相关主题的论文。我们的论文有四个主要贡献：

我们对 113 篇开创性的 IMG 论文进行了全面审查，并根据几个关键方面对其进行了评估：基础技术、应用范围、智能体学习目标、数据类型、目标挑战以及优势和局限性。
我们从三个不同的有利位置对现有的 IMG 方法进行了分类：关键技术、输出网格单元元素和合适的输入数据类型;
我们提供了与 IMG 密切相关的广泛概述，包括用于网格学习、网格质量评估和数据集;
我们概括了 IMG 目前面临的挑战，并概述了研究人员可以探索的潜在有前途的途径，以应对他们未来的努力中的挑战。

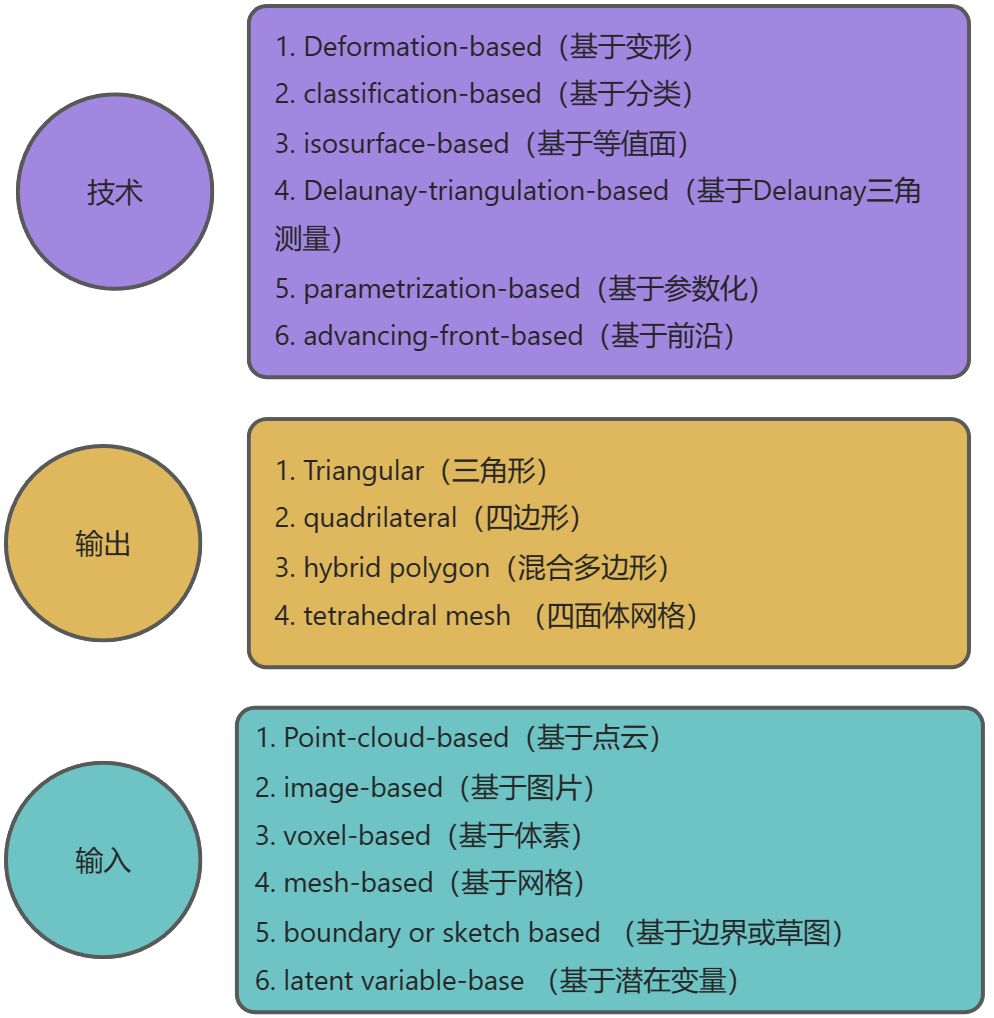
图 1：从三个角度对现有 IMG 方法进行分类。

方法

本文的目的是通过采用双管齐下的策略提供全面而系统的调查。在初始阶段，我们深入研究现有文献，使用开放式解释方法和以关键词为中心的文献综述筛选出与 IMG 相关的工作。前一种方法以作者的专业知识为基础，从而产生了广泛而探索性的作品集，尽管它可能会引入选择偏差。相比之下，后者针对特定的 IMG 出版物，提供了明确的边界，但其有效性在很大程度上取决于所选择的关键词。为了融合这两种方法的优势，我们随后应用了以关键词为中心的解释方法和开放式解释方法。在随后的阶段，我们根据提取的内容对第一阶段收集的所有文章进行编译和评估。

检索策略

检索策略对于收集有关特定主题的相关文献至关重要。搜索字符串和库的选择是重要因素。我们精心设计了一个检索字符串，并选择了五个不同的图书馆来寻找相关论文。遵循 SLR 准则 [2]，我们通过使用布尔运算符合并关键字及其同义词来构建搜索字符串。

关键字和布尔运算符：
- [(”computer graphics”OR ”computational geometry”) AND (”mesh reconstruc-tion” OR ”mesh generation” OR ”Surface reconstruction”OR ”3D object reconstruction” OR ”triangulation” OR ”quadri-lateral” OR ”tetrahedral” OR ”hexahedral”) AND (”intel-ligent” OR ”learning” OR ”data-based” OR ”neural net-work” OR ”ANN”)] OR (”mesh evaluation” OR ”3D object dataset” OR ”mesh neural network” OR ”mesh metric”)
- [（“计算机图形学”或“计算几何”）和（“网格重建”或“网格生成”或“表面重建”或“3D 对象重建”或“三角测量”或“四边形”或“四面体”或“六面体”）和（“智能”或“学习”或“基于数据”或“神经网络”或“ANN”）] 或（“网格评估”或“3D 对象数据集”或“网格神经网络”或“网格度量”）。

内容提取及结果呈现

现有文献提供了大量的 IMG 技术。我们共选取了 190 篇论文进行详细分析; 113 篇论文聚焦 IMG，77 篇论文深入探讨 IMG 相关领域，包括用于网格的经典神经网络、网格质量指标和网格数据集等。根据我们的研究问题，我们从每篇入选论文中摘录了以下细节：

面临的主要挑战和取得的重大突破;
基本概念、适用范围及利弊;
输入数据的类型、输出网格和网格质量。

此外，为了更客观地评估这些 IMG 方法，我们收集了以下附加信息：

文章的引用频率（根据谷歌学术引用每月的引用次数）;
本文所提算法的实用性。

从关键技术、输出网格类型和输入数据类型的角度，我们首先对已有的 IMG 论文进行了分类，并在表 1 中进行了介绍。该表还封装了 IMG 是否是端到端的、其主网络结构以及神经网络模型的学习目标。表 1 从三个独特的角度对 113 篇 IMG 论文进行了清晰的分类，从而可以直观地了解每种 IMG 方法中如何融入智能。其次，我们深入研究了每篇 IMG 论文的详细内容，并按时间顺序组织了表 2。下表列出了每项研究的目标挑战、优势、局限性和平均每月引用次数。我们还在图 2 中展示了一些具有代表性的方法，将现有的 IMG 论文整理成折线图。

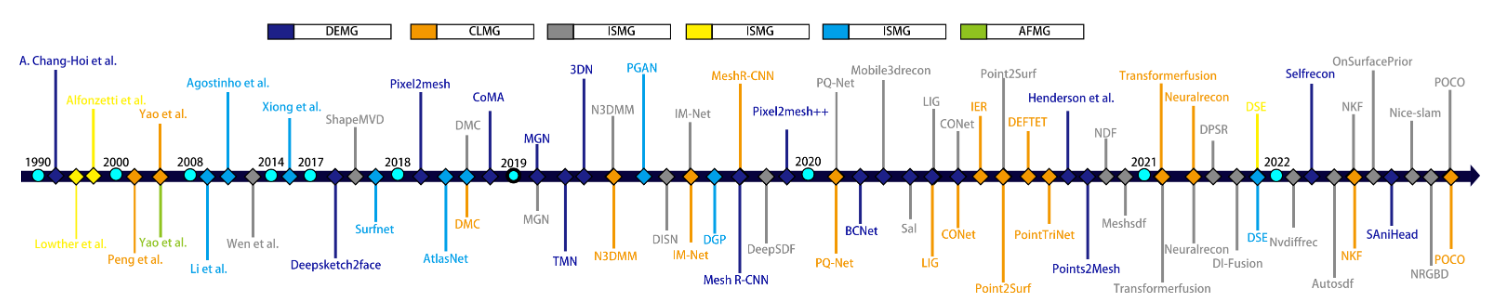
图 2：具有代表性的 IMG 方法的时间序列概述

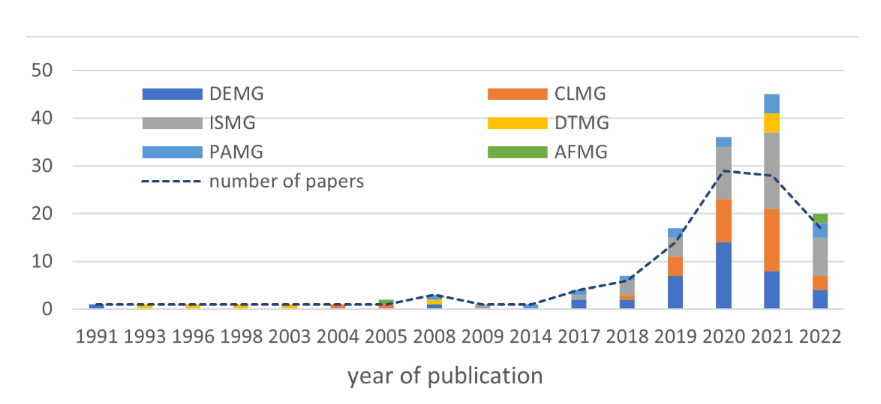
图 3：6 种技术类型文章的年度分布情况。

表 1：文献中使用的各种类型的 IMG 的分类。DEMG、CLMG、ISMG、DTMG，尽管只有具有简单 PAMG 和 AFMG 的平面网格分别表示基于变形、基于分类、基于等值面、基于德劳内三角剖分、基于参数化和基于前沿的网格生成。PC、IM、VO、ME、BS 和 LA 分别表示基于点云、基于图像、基于体素、基于网格、基于边界或草图以及基于潜在变量的 IMG。Tri、Qua、Hyb 和 Tet 分别表示三角形、四边形、混合多边形和四面体网格。E2E 表示端到端，✓ 表示满意。

Article(提议)	技术						输入						输出					描述
	DEMG(基于变形)	CLMG(基于分类)	ISMG(基于等值面)	DTMG(基于德劳内三角剖分)	PAMG(基于参数化)	AFMG(基于前沿)	PC(点云)	IM(图像)	VO(体素)	ME(网格)	BS(边界/草图)	LA(潜在变量)	Tri(三角网格)	Qua(四边形)	Hyb(混合多边形)	Tet(四面体)	E2E(端到端)	Network Structure(网络结构)	Learning Goals(学习目标)
Self-organizing [42]	✔️										✔️		✔️	✔️			✔️	Self-organizing network	Vertices location（顶点位置)
Lowther et al. [43]				✔️							✔️		✔️					Feed forward net	Element size（元素大小）
Alfonzetti et al. [44]				✔️						✔️			✔️					Let-It-Grow ANN	Node position（节点位置）
Alfonzetti et al. [45]				✔️						✔️			✔️					ANN	Node location（节点位置）
Alfonzetti et al. [46]				✔️						✔️			✔️			✔️		ANN	Node position（节点位置）
Peng et al. [47]		✔️					✔️						✔️				✔️	MLP	Coordinate z；Point occupancy（坐标 z；点占用）
Yao et al. [48]		✔️				✔️					✔️			✔️			✔️	ANN	Node position（节点位置）
Alfonzetti et al. [49]				✔️						✔️			✔️					Let-It-Grow ANN	Node position（节点位置）
Li et al. [50]					✔️		✔️						✔️					RBFs network	Radial basis function（径向基函数）
Agostinho et al. [51]					✔️		✔️						✔️				✔️	Self-organizing map	3D coordinates（3D 坐标)
Wen et al. [52]			✔️				✔️						✔️					RBFs network	Radial basis function（径向基函数）
Xiong et al. [53]					✔️		✔️						✔️				✔️	Sparse dictionary	Vertex position and triangulation（顶点位置和三角剖分）
DeepGarment [8]	✔️							✔️					✔️				✔️	SqueezeNet	Vertex location（顶点位置）
Deepsketch2face [9]	✔️										✔️		✔️				✔️	AlexNet	Vertex position（顶点位置）
ShapeMVD [54]			✔️								✔️		✔️					U-net	Depth and normal map（深度和法线图）
Surfnet [55]					✔️			✔️					✔️					Res-Unet	Geometric image（几何图像）
Pixel2mesh [10]	✔️							✔️					✔️				✔️	GCN; VGG-16; MLP	Vertex coordinates；Feature extraction（顶点坐标；提取特征）
AtlasNet [56]					✔️		✔️	✔️					✔️					PointNet/ResNet+MLPs	Point location（点位置）
Li et al. [57]			✔️								✔️		✔️					U-Net	Normals, depth map（法线、深度图）
DMC [58]		✔️	✔️				✔️						✔️				✔️	DMC	Occupancy and vertex displacement（占用和顶点位移）
CoMA [59]	✔️											✔️	✔️				✔️	Autoencoder	Point location（点位置）
3D-CFCN [60]			✔️				✔️						✔️					OctNet-based U-Net	Truncated signed distance field（截断有符号距离场）
MGN [11]	✔️				✔️			✔️					✔️				✔️	MLP	Vertex position（顶点位置）
3DN [35]	✔️						✔️	✔️					✔️				✔️	PointNet/VGG	Vertex position（顶点位置）
TMN [12]	✔️							✔️					✔️				✔️	ResNet/MLP	Vertex position and error（顶点位置和误差）
ONet [61]		✔️	✔️				✔️	✔️	✔️				✔️					ResNet/PointNet	Grid occupancy（网格占用）
N3DMM [62]	✔️											✔️	✔️				✔️	Spiral-Conv GAN	Vertex position（顶点位置）
PGAN [63]					✔️							✔️	✔️					WGAN	Geometric image（几何图像）
HumanMeshNet [13]	✔️							✔️					✔️				✔️	Resnet-18	Vertex position（顶点位置）
DISN [64]			✔️				✔️	✔️					✔️					VGG-16	Signed distance field（有符号距离场）
IM-Net [65]		✔️	✔️				✔️	✔️					✔️					IM-Net	Signed distance field（有符号距离场）
Scan2Mesh [66]		✔️							✔️				✔️				✔️	3D-Conv GNN	Mesh faces（网格面片）
DGP [67]					✔️		✔️						✔️				✔️	MLP	Local parameterization（局部参数化）
Mesh R-CNN [14]	✔️	✔️						✔️					✔️					Mesh R-CNN	Occupancy and point location（占用和点位置）
DeepSDF [68]			✔️				✔️						✔️					MLP	Signed distance field（有符号距离场）
Pixel2mesh++ [15]	✔️							✔️					✔️				✔️	VGG; GCN	Vertex position（顶点位置）
PQ-Net [69]		✔️	✔️					✔️				✔️	✔️					Seq2Seq Autoencoder	Signed distance field（有符号距离场）
BCNet [16]	✔️							✔️					✔️				✔️	ResNet; GAT; Spiral-Conv	SMPL parameters(SMPL 参数); Vertex position（顶点位置）
PolyGen [70]		✔️						✔️	✔️						✔️		✔️	Transformer-based	Predict vertices and faces sequentially(按顺序预测顶点和面)
DGTS [71]	✔️									✔️			✔️				✔️	GCN	Displacement vector for each face（每个面的位移向量）
Neural Subdivision [72]	✔️									✔️			✔️				✔️	MLP	Predicting vertex positions（预测顶点位置）
Mobile3drecon [73]			✔️					✔️					✔️					Res-UNet	Depth map（深度图）
Sal [74]			✔️				✔️						✔️					MLP	Unsigned distance field（无符号距离场）
Pixel2mesh2 [17]	✔️							✔️					✔️				✔️	GCN; G-Resnet	Vertex position（顶点位置）
Voxel2mesh [40]	✔️								✔️				✔️				✔️	GCN-3D	Vertex position（顶点位置）
X-ray2shape [18]	✔️							✔️					✔️				✔️	CNN; GCN	Vertex position（顶点位置）
Li et al. [19]	✔️							✔️					✔️				✔️	Resnet; 3D-GCN	Vertex position（顶点位置）
Meshlet [75]			✔️		✔️		✔️						✔️					FC-based AE	Vertex position（顶点位置）
LIG [76]		✔️	✔️				✔️						✔️					AE; 3D-CNN; Residual block	truncated signed distance field（截断有符号距离场）
CONet [77]		✔️	✔️				✔️						✔️					U-Net	Grid occupancy probability（网格占用概率）
ILSM [78]		✔️	✔️								✔️		✔️					CGAN	Occupancy(占用）; Velocity field（速度场）
IER [79]		✔️					✔️						✔️				✔️	SpareConv; MLP	Triangle classification（三角形分类）
Yang et al. [20]	✔️							✔️					✔️				✔️	VGG16; GCN; Graph attention	Vertex position（顶点位置）
MeshingNet [21]	✔️										✔️		✔️				✔️	FCN/Resnet	Vertex position（顶点位置）
Point2Surf [80]		✔️	✔️				✔️									✔️		MLP	Signed distance field（有符号距离场）
DEFTET [81]		✔️					✔️	✔️					✔️					MLP;	Occupancy prediction（预测占用）
BTM [36]	✔️						✔️						✔️					Autoencoder	Initial mesh（初始网格）
PointTriNet [82]		✔️					✔️						✔️				✔️	MLP	Triangle labels（三角形标签）
Surface Hof [22]	✔️							✔️					✔️				✔️	AE	Vertex position（顶点位置）
REIN [83]		✔️					✔️						✔️				✔️	GraphRNN	Edge prediction（边预测）
Henderson et al. [23]	✔️							✔️					✔️				✔️	CNN	Vertex position（顶点位置）
SSRNet [84]			✔️				✔️						✔️					UNet; tangent convolution	Octree vertex labels（八叉树顶点标签）
MeshVAE [85]	✔️											✔️	✔️				✔️	CVAE; GCN	Vertex position（顶点位置）
Point2Mesh [37]	✔️						✔️						✔️				✔️	GCN	Vertex position（顶点位置）
NMF [38]	✔️						✔️	✔️					✔️				✔️	Conditional Flow/PointNet	Vertex position（顶点位置）
NDF [86]			✔️				✔️						✔️					IF-Nets	Unsigned distance field（无符号距离场）
Meshsdf [87]			✔️					✔️					✔️				✔️	SplineCNN	Vertex position（顶点位置）
Smirnov et al. [26]	✔️				✔️						✔️			✔️				ResNet-18	Local parameterization（局部参数化）
Lasr [24]	✔️							✔️					✔️				✔️	Flow/Mask Nets	Vertex position（顶点位置）
Transformerfusion [88]		✔️	✔️					✔️					✔️					Transformer; 3D-CNN	Learning occupancy field（学习占用场）
CSPNet [89]		✔️	✔️				✔️						✔️					CONet; PointNet	Unsigned distance field（无符号距离场）
DASM [25]	✔️							✔️					✔️				✔️	GCN; Mesh R-CNN	Vertex position（顶点位置）
Neuralrecon [90]		✔️	✔️					✔️					✔️					GRU; MLP	Truncated signed distance field（截断有符号距离场）
Sa-convonet [91]		✔️	✔️				✔️						✔️					PointNet;	CNN learning occupancy field（CNN 学习占用场）
DMTet [92]			✔️				✔️		✔️				✔️				✔️	CGAN	Vertex position；Signed distance field（顶点位置；有符号距离场）
Vis2mesh [93]		✔️		✔️			✔️						✔️					U-Net; PConv	Visibility map（可见性图）
IMLSNet [94]		✔️	✔️				✔️						✔️					Octree based CNNs	Signed distance field（有符号距离场）
Retrievalfuse [95]			✔️				✔️						✔️					U-net; Attention	Truncated distance field（截断距离场）
Deepdt [96]		✔️	✔️				✔️						✔️					GCN	Interior-exterior classification（内外分类）
Iso-points [97]			✔️		✔️		✔️	✔️					✔️					IDR	Isosurface（等值面）
DST [98]				✔️			✔️						✔️				✔️	–	Parameterization（参数化）
SAP [99]			✔️				✔️						✔️					MLP	Mesh indicator function（网格指示函数）
Bertiche et al. [27]	✔️							✔️					✔️				✔️	Point-CNN	SMPL parameters；Vertex position（SMPL 参数；顶点位置）
NeeDrop [100]		✔️	✔️				✔️						✔️					ONet	Interior-exterior classification（内外分类）
LMR [28]	✔️							✔️					✔️				✔️	RNN;	SMPL parameters（SMPL 参数）
NRSfM [29]	✔️							✔️						✔️			✔️	Unet	Point location（点的位置）
AnalyticMesh [101]		✔️	✔️				✔️								✔️		✔️	MLPs	Isosurface（等值面）
DHSP [102]	✔️				✔️		✔️						✔️					MeshCNN; 2DCNN	Vertex position；Texture mapping（顶点位置；纹理映射）
Neural-Pull [39]			✔️				✔️						✔️					MLP	Signed distance field（有符号距离场）
DI-Fusion [103]			✔️					✔️					✔️					MLP based AE	Truncated signed distance field（截断有符号距离场）
DSE [104]				✔️	✔️		✔️							✔️				FoldingNet	Parameterization（参数化）
LDFQ [105]					✔️					✔️			✔️					Pointnet; SpiralNet	Direction field（方向场）
DGNN [106]		✔️		✔️			✔️						✔️				✔️	GNN+MLP	Tetrahedral interior-exterior score（四面体内外得分）
Hu et al. [30]	✔️							✔️					✔️				✔️	GAN	Mesh texture（网格纹理）
NMC [107]		✔️	✔️						✔️				✔️				✔️	MLP	Isosurface（等值面）
Skeletonnet [32]	✔️	✔️	✔️					✔️					✔️					Point2voxel; 3D-Unet	Interior-exterior classification（内外分类）
Nvdiffrec [108]			✔️					✔️					✔️				✔️	GAN; MLP	Signed distance field；Texture（有符号距离场；纹理）
Selfrecon [33]	✔️							✔️					✔️					MLP	Point position and isosurface（点位置和等值面）
Autosdf [109]			✔️					✔️					✔️					VQ-VAE; transformer	Signed distance field（有符号距离场）
NKF [110]		✔️	✔️				✔️				✔️		✔️					CNN	Interior-exterior classification（内外分类）
Sketch2PQ [111]					✔️									✔️			✔️	U-Net	Spline surface and direction field（样条曲面和方向场）
SRMAE [112]	✔️									✔️			✔️				✔️	AE; 2DConv	Hexagonal mesh position（六边形网格位置）
OnSurfacePrior [113]			✔️				✔️						✔️					MLP	Signed distance field（有符号距离场）
Lu et al. [114]						✔️					✔️				✔️		✔️	BP-ANN	Node position；Angle（节点位置；角度）
MGNet [115]					✔️						✔️			✔️			✔️	MLPs	Point position（点的位置）
RLQMG [116]						✔️					✔️			✔️			✔️	RL; FNN	Point position；Insertion type（点的位置；插入类型）
TopoNet [34]	✔️							✔️					✔️				✔️	pixel2mesh; GCN; RL	Point position；Face occupancy（点的位置；面占用）
SAniHead [41]	✔️										✔️		✔️				✔️	Pixel2mesh; GCN	Point position（点的位置）
NDC [117]		✔️	✔️				✔️		✔️				✔️				✔️	3D CNN/pointnet++	Edge prediction（预测边）
PCGAN [118]					✔️							✔️	✔️					GAN	Geometric image（几何图像）
Nice-slam [119]			✔️					✔️					✔️					MLPs	Isosurface（等值面）
NRGBD [120]			✔️					✔️					✔️					NeRF	Signed distance field（有符号距离场）
POCO [121]		✔️	✔️				✔️						✔️					FKAconv；Attention model	point occupancy（点占用）

表 2：所有选定的 IMG 方法的提议、优势和局限性。AMC 表示平均每月引用次数

（Article）论文	Challenges (提议)	Advantages (优势)	Limitations (局限性)	AMC（引用次数/每月）
Self-organizing [42]	非均匀密度网格生成	生成具有指定密度分布的网格	仅处理具有给定边界的简单情况	0.12
Lowther et al. [43]	非均匀密度网格生成	完全自动，密度自适应网格	结果极不规则，需要边界	0.08
Alfonzetti et al. [44]	非均匀密度网格生成	密度自适应网格；保留边界	需要一个初始粗略网格	0.12
Alfonzetti et al. [45]	非均匀密度网格生成	顶点密度函数可以自适应计算	需要一个初始粗略网格	0.07
Alfonzetti et al. [46]	非均匀四面体网格生成	可以生成预设数量的四面体网格	需要一个粗糙的初始网格和密度函数	0.04
Peng et al. [47]	手动表示复杂的 3D 物体	将多层感知器与 3D 对象重建相结合	MLP 只需要恢复 Z 坐标	0.14
Yao et al. [48]	规定 IMG 网格元素提取规则	在一定程度上减少奇点的数量	不是端到端的；可能陷入局部最小值	0.16
Alfonzetti et al. [49]	为 3D 情况生成高质量网格	输出网格质量好；算法简单	仅处理具有给定边界的简单情况	0.04
Li et al. [50]	对不完整输入数据的鲁棒性	不完整点云数据的表面重建	神经网络仅用于补充点云	0.02
Agostinho et al. [51]	详细的多分辨率网格生成	以多分辨率方式；只需要一个简单的初始网格	仅适用于 0 类对象网格的生成	0.25
Wen et al. [52]	RBF 方法中的病态矩阵和过拟合问题	克服系数矩阵的数值病态和过拟合问题	径向基函数的选择限制了隐式函数的解空间	0.05
Xiong et al. [53]	克服多阶段处理的限制	联合优化几何和连接性；对异常值和噪声具有鲁棒性；保留尖锐特征	不能保证收敛；无法避免局部最小值；可能在孔区域失败	0.69
DeepGarment [8]	智能、高效和实用的 IMG	仅从单个图像中高效捕获 3D 服装形状	仅能处理简单的 T 恤和连衣裙	0.89
Deepsketch2face [9]	将草图转换为网格	有效地推断 2D 草图的网格；有效地帮助用户创建面部网格	仅适用于卡通模型；无法创建皱纹等细节	1.74
ShapeMVD [54]	转换草图为网格的高效性	输出网格保留拓扑和形状结构	输出网格缺乏细节；非端到端可微分	2.47
Surfnet [55]	直接生成刚性和非刚性形状的网格	在一定程度上解决面积畸变问题	仅能生成 0 类曲面	2.60
…	…	…	…	…
Pixel2mesh [10]	输出网格丢失表面细节	肯定保留表面细节	仅能重建与初始网格拓扑类似的对象	16.82
AtlasNet [56]	生成高分辨率的 3D 形状	生成任意分辨率的形状；适用范围广	存在失真或重叠	16.29
Li et al. [57]	从 2D 草图建模通用自由曲面 3D 表面	自由曲面建模；只需要简洁的线条注解；解决流场问题	无法创建几何细节；每次只能建模一个补丁；不是端到端可微分的	1.22
DMC [58]	立方体算法端到端	立方体网格端到端生成；	高内存要求；受限于
体素分辨率	3.04
CoMA [59]	生成人脸的 3D 网格	生成多样逼真的 3D 人脸；	需要来自相同对象类的参考模板	6.60
3D-CFCN [60]	不完整和噪声输入	在一定程度上，对噪声鲁棒；	薄片的网格生成较差	0.50
MGN [11]	预测物体几何结构	重建网格并捕捉纹理；	无法处理姿态相关的变形；依赖分割	5.03
3DN [35]	简单高效的 IMG 算法	端到端可优化模型；	需要参考模板	2.23
TMN [12]	高质量网格生成	可重建各种拓扑的网格；	无法直接生成未封闭表面	3.12
ONet [61]	简单高效的网格表示	能在任何分辨率提取 3D 网格；可以处理各种输入	高内存要求	28.79
N3DMM [62]	网格的高效特征表示	创建各向异性网格；轻便易优化模型；	需要来自相同对象类的参考模板	2.48
PGAN [63]	探索几何图像的网格生成	生成多样逼真的 3D 人脸；	复杂的预处理/后处理；参数化导致网格失真	0.03
HumanMeshNet [13]	实时重建	确保光滑的表面重建；	训练数据和测试数据必须是相同的基本模型	0.35
DISN [64]	高质量和详细的网格生成	捕捉细粒度细节；	只能处理有明确背景的对象	8.45
IM-Net [65]	生成高视觉质量的网格	有效的坐标信息表示；	很多非表面点导致无效计算	17.10
Scan2Mesh [66]	适应不完整扫描	从嘈杂和部分范围扫描中生成更加干净和类 CAD 的网格	高内存要求；不强制网格的规则性和连续性	1.67
DGP [67]	稠密重建点云	对噪声鲁棒；捕捉锐利特征；任意分辨率的网格	高计算复杂度；没有自适应补丁选择	2.59
Mesh R-CNN [14]	高质量和详细的网格生成	适用于无约束的现实世界图像；	非流形，重建精度低	8.03
DeepSDF [68]	在保真度、效率和压缩能力之间进行取舍	实现高质量的形状表示、插值和从部分和嘈杂的 3D 输入数据中完成	简单的全连接网络结构，没有局部信息或平移等变性	32.23
Pixel2mesh++[15]	跨视图信息融合	利用跨视图信息；强大的泛化能力；	仅能生成 0 亏格的表面	3.74
PQ-Net [69]	本地结构和几何编码	学习以顺序部件装配的形式的 3D 形状表示；	不能学习对称关系或产生改变拓扑的网格	2.15
BCNet [16]	几何表示的准确性	能生成不同拓扑的服装；	一些细节无法生成	2.48
PolyGen [70]	生成多样逼真的几何形状	能生成连贯且多样化的网格样本；	适用于生成人造物体表面，但不适用于复杂曲面的生成	3.68
DGTS [71]	学习网格的几何信息	在不同拓扑的两个曲面之间转移几何信息；不需要参数化	无法有效学习整体语义信息；对输入数据有较高要求	1.30
Neural Subdivision [72]	生成光滑且保持特征的细分结果	能学习复杂的非线性细分方案；	无法保证全局语义信息	1.83
Mobile3drecon [73]	实时网格生成	实时稠密网格重建；	对锐利特征的维护较差	3.33
Sal [74]	适用于无符号几何数据	不需要地面真实法向数据或内/外标记；	对薄部位的生成不佳	7.30
Pixel2mesh2 [17]	保留表面细节	几何正则化约束；	仅适用于 0 次亏格表面	0.76
Voxel2mesh [40]	无需后处理	能生成无需任何后处理的 3D 网格；	仅适用于 0 次亏格表面	1.39
X-ray2shape [18]	适用于低对比度图像数据	对低对比度图像有效；	太多的奇点；无法处理复杂拓扑	0.30
Li et al.[19]	背景重建	最终网格不受环境影响；预处理决定网格质量；	薄部位生成不佳	0.02
Meshlet [75]	对稀疏和嘈杂的 3D 点稳健	适用于稀疏嘈杂数据；规则且全局一致的网格；	对薄结构失败；分辨率固定	1.08
LIG [76]	用于规模和复杂室内场景的 IMG	能生成任意规模带有细节的场景的网格；	假设不同类别共享相似的部分几何	7.85
CONet [77]	可扩展和复杂场景网格生成	整合局部和全局信息；获得平移等变性；	不适用于稀疏点云和对噪声不稳健	13.59
ILSM [78]	逼真的液体飞溅网格生成	从简单用户草图输入生成逼真的液体飞溅网格；	无法生成像真实世界飞溅那样的详细飞溅；泛化能力弱	0.22
IER [79]	生成精细的细节；泛化能力强	保留细节；处理模糊结构；泛化能力强；	非流形网格有孔洞；需要后处理	0.83
Yang et al.[20]	生成物体细节	端到端架构	仅适用于 0 次亏格形状	0
MeshingNet [21]	自动非结构化网格生成	非均匀网格生成方法；将 PDEs 与 IMG 结合；	仅测试了平面网格生成	0.81
Point2Surf [80]	处理部分扫描和噪声	适用于不均匀嘈杂的输入和具有不同拓扑的对象；	不是端到端可微分的过程	2.73
DEFTET [81]	单图像到四面体网格的生成	适用于任何拓扑；高效算法；无需后处理；	有翻转的四面体；无法保证特征	1.38
BTM [36]	单一网格原型的泛化能力	比可比方法更具泛化能力；	高计算复杂度，需要多个网格原型	0.10
PointTriNet [82]	高效、可扩展和泛化的算法	以无监督方式训练；对异常值具有鲁棒性；	有很多孔洞的网格，非流形	1.04
Surface Hof [22]	高分辨率表面重建	为各种拓扑生成任意分辨率的详细网格；	仅适用于有明确背景的图像；不是端到端可微分的	0.10
REIN [83]	用稀疏点云生成网格	稀疏点云的网格生成	非流形，无置换不变性	0.04
Henderson et al. [23]	产生纹理网格	没有自相交点; 不需要真实值分割 masks	需要具有相同拓扑结构的引用模板	1.83
MeshVAE [85]	一种有效的网格池化操作	基于网格简化的池操作; 可以生成细节	仅适用于均匀网格; 非水密或不规则网格会失败	0.65
Point2Mesh [37]	网格生成的可学先验方法	对无方向法线和噪音具有稳健性; 产生水密网格，非监督式学习	需要初始网格; 高计算复杂度和重建精度低	3.68
SSRNet [84]	大规模点云网格重建	强大的可扩展性；擅长重建几何细节	不是一个端到端可微的过程；分区方法至关重要	1.26
NMF [38]	流形网格生成	生成两个流形网格	只适用于 0 亏格形状	1.26
NDF [86]	任意形状的高分辨率输出	可以生成非闭合的表面；可以表示内部结构	网格划分需要后处理	3.67
Meshsdf [87]	曲面网格生成的一种可微方法	端到端可微；任意拓扑结构的水密网格	泛化性能不足，仅生成简单网格	2.19
Smirnov et al. [26]	高效的 IMG	最终网格具有较少的异常点	需要后处理	0.87
Lasr [24]	非刚性结构网格生成	不需要特定类别的网格模板；良好的通用性	在严重遮挡时失败；效率需要改进	1.47
Transformerfusion [88]	高效的编码和准确的重建	交互式帧率运行的在线重建方法	在某些场景中无法构建细节；	2.36
CSPNet [89]	为复杂表面提供高效且低内存占用的表示	可表示任意拓扑的复杂表面；局部几何属性的高效计算	不是端到端可微的过程	0.82
DASM [25]	利用局部正则化	插拔式平滑模块可以生成更平滑的网格	网格平滑需要手动设计的度量	0.47
Neuralrecon [90]	精确、一致和实时重建	可以实时生成精确和连贯的重建	不是端到端可微的过程	2.93
Sa-convonet [91]	可扩展到大规模场景；通用性	适用于大型场景；	推断速度慢	1.18
DMTet [92]	从 IMG 生成高质量和详细的网格	可以生成任意拓扑的网格，更精细的几何细节，较少的伪影	全局均匀分辨率；容易产生双层/断裂表面	0.81
Vis2mesh [93]	大规模场景网格生成	良好的泛化性；对噪声鲁棒；细节重建	系统复杂	0.09
IMLSNet [94]	将离散点集转换为光滑网格	在点集上定义隐式函数	不是端到端可微的过程	1.60
Retrievalfuse [95]	大场景网格重建	精确的场景重建；保留局部细节	检索结果可能不够理想	1.27
Deepdt [96]	内部/外部分类无法获得干净的网格	没有四面体的真实标签或可见性信息	无法处理过大的输入	0.47
Iso-points [97]	用于嘈杂和不完整输入的 IMG	更快的收敛和准确的细节和拓扑恢复	没有明确地建模外观	0.87
DST [98]	三角网格的可微结构	控制顶点位置和拓扑；对顶点数量线性复杂度	需要表面分割；边界上存在可见的伪影；无法处理大量点或部件	0.38
SAP [99]	点到网格层的高效可微表示	输出无漏洞流形网格；可解释，轻量级和短推理时间；对异常值鲁棒	仅限于小型场景；需要立方级别内存	1.60
Bertiche et al. [27]	对各种几何和拓扑的泛化性	具有微分几何的连续预测	最终网格中缺少服装细节	0
NeeDrop [100]	用极度稀疏的点云生成网格	自监督方法；输入数据可以是稀疏点云	需要后处理生成网格	0.33
AnalyticMesh [101]	精确的网格重建	与 Marching Cube 相比不丢失隐式场的细节	需要后处理，如平滑或填补孔	0
LMR [28]	在野外视频中的网格推断	视频网格恢复的局部动力学建模方法	生成的网格无法匹配人体	0
NRSfM [29]	非刚性表面重建	用于非刚性变形网格生成的简单有效模型	生成的网格可能在面片边界重叠	0.11
DHSP [102]	用稀疏彩色点云生成网格；多先验集成	生成具有高分辨率纹理的网格；稀疏噪声点云鲁棒	结构和操作复杂；仅能处理简单拓扑的单个物体模型	0.27
Neural-Pull [39]	学习高质量 SDF 以生成网格	无需符号距离值学习 SDF；对噪声鲁棒	重建网格中缺少清晰的特征	1.30
DI-Fusion [103]	内存和网格质量之间的权衡	同时编码几何和不确定信息；	无法保持空间连续的尖锐特征	1.47
DSE [104]	生成流形网格	产生近流形的三角网格，对异常值鲁棒	不是端到端可微的；需要对部件进行对齐	0.67
LDFQ [105]	四边形的 IMG 方法依赖于稠密的用户提供的方向场	对计算方向场的稳健数据驱动方法	构造框架场的真实值的构建方式决定网格的质量	0.09
DGNN [106]	用于大规模场景和不完整点云输入的 IMG	大规模、缺陷点云的网格重建；考虑可见性信息	通用性低，在采集噪声较大、重建细节缺失时限制精度	0.17
Hu et al. [30]	生成复杂的几何特征	在网格密度和特征表示之间取得权衡	最终网格有更多重叠	0.07
NMC [107]	保留尖锐特征的 IMG 方法	可保持尖锐的几何特征和学习局部拓扑	对旋转敏感；生成的网格可能出现自相交	0.89
Skeletonnet [32]	拓扑上的约束不足	保留拓扑；高质量的骨架体积	无法处理野外自然图像；算法复杂度高	0.80
Nvdiffrec [108]	拓扑、材质和光照的联合优化	具有材质的外观感知和端到端的网格生成	计算和内存消耗高；简化着色模型	3.33
Selfrecon [33]	结合隐式和显式表示的优势	通过自监督优化为穿着服装的人产生高保真度表面	优化时间长；主要适用于自旋转运动	2.00
Autosdf [109]	网格生成的强大先验	对多种任务的多模态生成有用；对齐敏感；	仅适用于 CAD 模型；不是端到端可微的	3.67
NKF [110]	用稀疏点云生成大场景网格；通用性	能够重建训练集之外的形状类别；能够重建大场景网格	核实现需要密集线性求解；需要定向点	2
Sketch2PQ [111]	实时 IMG	带有密集方向场的实时网格生成	不是端到端可微的；仅适用于圆盘拓扑表面	0
SRMAE [112]	良好的泛化性	能够处理不同尺寸的网格；适用于无边界网格	繁琐的预处理；全局信息利用不足	0.25
OnSurfacePrior [113]	用稀疏点云和有效先验生成网格	不需要 SDF 和法线；适用于稀疏点云	不是端到端可微的过程	1.33
Lu et al. [114]	智能前沿法	一种基于自动化前沿的 IMG 方法	仅适用于 2D 网格；缺少对异常点的控制；	0
MGNet [115]	差分结构网格生成	无监督结构四边形网格生成；无需先验知识或测量数据	边界精度决定网格质量；只适用于平面网格	0.33
RLQMG [116]	高效智能的四边形网格生成	无需额外清理操作即可自动生成四边形网格	缺少对异常点的控制；仅适用于平面网格生成	0.20
TopoNet [34]	拓扑通用性	不受模板拓扑限制；更好地捕捉几何形状	重建的网格中有小孔	0
SAniHead [41]	动物头部的网格生成	能够生成具有几何细节的网格	难以创建具有细小结构和较差泛化能力的形状	1.33
NDC [117]	对双轮廓方法难以获得表面梯度	良好的重建质量；适用于各种输入	生成非流形网格，对方向不完全不变	0
PCGAN [118]	通过 CNN 处理网格之间的拓扑相似性	保留拓扑信息和空间结构；	需要为网格生成进行预处理和后处理	0
Nice-slam [119]	大场景过度平滑的网格生成	能够填补小孔并外推场景几何；实时系统	只有粗略表示	4.33
NRGBD [120]	室内场景高质量网格重建	有效结合深度观测和神经辐射场进行室内场景重建	需要后处理；缺乏细节；收敛慢	8.67
POCO [121]	隐式重建的可扩展性	既适用于单个对象重建，也适用于整个场景重建	缺少大型部件时无法完成形状; 如果没有法线，则定位失败	2.00

基本概念

通常，网格分为曲面网格和体积网格。曲面网格是一组多边形面，目标是形成对象曲面的近似值。多边形曲面网格具有三种不同的组合元素：顶点、边和面。这个网格也可以被认为是几何和拓扑的组合，其中几何提供了它所有顶点的位置，而拓扑提供了不同相邻顶点之间的信息。在数学上，包含
顶点和
面的多边形曲面网格
形成为

其中
是顶点集，
是面集，
的形成为:

其中
表示每个体素
的面数。

为了避免歧义，网格生成的定义如下：

定义 1.网格生成：
- 网格生成就是这样一个任务：给定输入数据
  ，映射
  并输出曲面网格
  或体积网格

从本质上讲，网格生成的目标是恢复
中缺失的几何信息或拓扑信息。通过我们的调查现有 IMG 方法的输入数据类型不会超出点云、图像、体素、边界或草图、网格和潜在变量。

基于技术的分类

在本节中，我们将现有的 IMG 方法分为六组，即基于变形的、基于分类的、基于等值面的、基于 Delaunay 三角测量的、基于参数化的和基于前沿的网格生成。这种分类基于每种方法固有的关键技术和指导原则。在这个分类中，我们说明了主要的 IMG 方法如何巧妙地将传统的网格生成技术与新的深度学习模块相结合，突出了每种方法的优点和缺点。我们预计这种分类法将帮助读者更直观地掌握神经网络在网格生成中的功能。

在基于变形的 IMG 算法中，神经网络模块主要预测顶点位置。
对于基于分类的 IMG，神经网络主要用作确定顶点连接或占用的分类器。
基于等值面的 IMG 采用神经网络进行隐式函数拟合和零等值面提取。
在基于 Delaunay 三角测量的 IMG 中，神经网络被用于预测顶点坐标或权重。
对于基于参数化的 IMG 算法，神经网络学习参数化映射或处理参数化数据。
在推进基于前端的 IMG 算法中，利用神经网络来预测波的正向和新节点的连接类型。

下文相应小节将作进一步阐述。

基于变形的网格生成

网格由多边形组成，本质上是连续表面的离散表示。多边形的组合性质阻止了在任何给定表面的可能网格划分空间上取导数。因此，网格处理和优化技术很难利用现代优化框架的模块化梯度下降组件。为了规避这个问题，基于变形的 IMG 引起了更多的关注。如图 4 所示，该技术的一个显着特征是需要初始网格，例如球形或椭球形模板网格。基于变形的 IMG 适用于不同类型的输入。基于几何信息的目标网格通常由图像 [8]–[34]、点云 [35]–[39] 或体素 [40]、[41] 生成。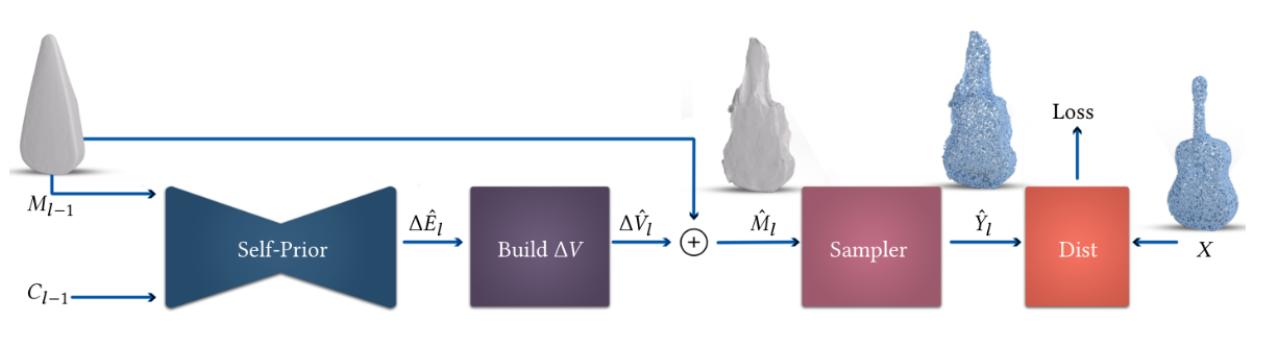
图 4：Point2Mesh [37]：一种基于变形的 IMG 方法

由于存在初始网格，这种类型的方法在一定程度上降低了网格生成的难度。神经网络只需要预测顶点的位置，因为连接关系已经存在。最早的基于变形的 IMG 工作可追溯到 1991 年，Ahn 等 [42] 提出了一种自组织神经网络来自动生成非均匀密度网格。这是一项开创性的工作，尽管只是平面网格与简单的几何学。近年来，出现了大量的实用方法。早期基于变形的 IMG 工作大多涉及对基本模型进行变形以获得目标网格，如服装 [8]、面部 [9] 和身体 [13]。这些方法仅生成特定目标对象的变形网格。后来，以 Pixel2Mesh [10] 为代表的一系列算法引入了模板作为基本网格，大大提高了实用性和泛化性。基于变形的方法与 GCN 和 MLP 紧密集成，以更好地预测顶点位置。然而，所有基于变形的模型都有一个共同的缺点：它们只能生成与初始网格具有相同拓扑结构的网格。因此，另一个研究方向是如何使其适应多种拓扑结构。Rios 等人。[36] 提出了一个非常直接的解决方案，即提供多个基本模板网格供算法自动选择。值得注意的是，这种方法并不能从根本上解决上述问题，而只是缓解了这些问题。为了继续，Charrada 等人。[34] 引入了一种面部修剪机制，该机制使用面部修剪操作迭代调整网格的拓扑结构，同时保留模板的主要属性，即吸引人的视觉外观和均匀的网格连接。诚然，面部修剪机制可以使该方法适用于更复杂拓扑的网格生成。

基于分类的网格生成

在结构化数据领域分类模型的启发和鼓励下，许多研究人员通过将基于分类模型的神经网络与网格生成相结合，设计了各种有效的 IMG 算法。这些算法分为两类：占用预测 [14]、[32]、[47]、[58]、[61]、[65]、[69]、[76]–[78]、[80]、[81]、[88]–[91]、[93]、[94]、[96]、[100]、[101]、[106]、[107]、[110]、[117]、[121] 和网格基本单元预测 [66]、[79]、[82]、[83]。前者对三维空间进行体素化，决定体素是否属于一个物体，这是一个二元分类问题。或者，占有预测可以进一步看作是物体的内部、表面和外部三个分类问题。后者将网格生成视为基本元素的组合，因此生成模型只需要判断要检测的基本元素是否应该存在，本质上也是一个二元分类问题。示例包括分面存在和局部连通性的分类。除了二元分类之外，还可以设计多分类来生成网格，例如 IER [79]。图 5 和图 6 分别显示了基于占用率和基本元素分类的 IGM 方法。

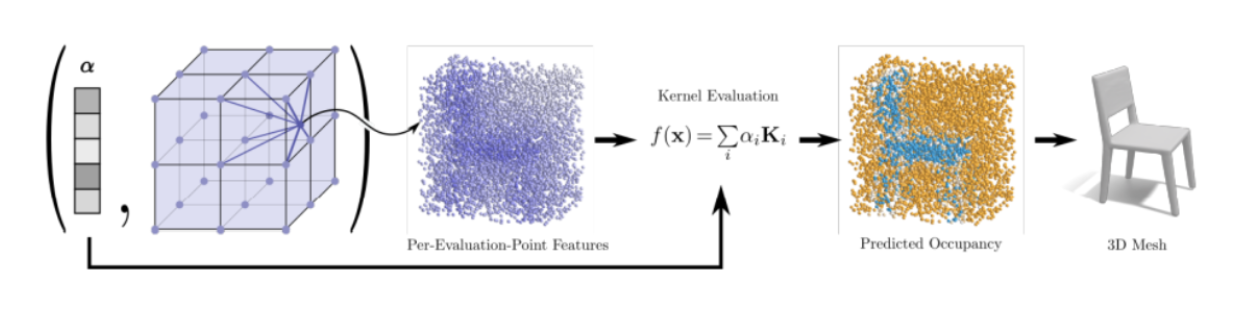
图 5：早期作品通过判断每个网格的占用来定位物体表面，然后重建图 5：NKF [110]：基于占用分类的 IMG。

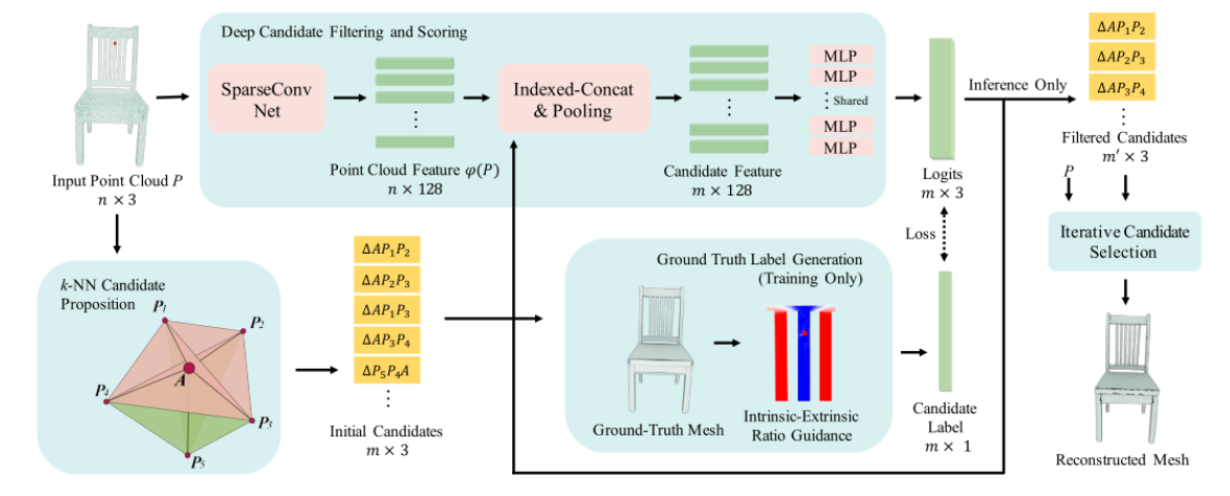
图 6： IER [79]：基于分面存在分类的 IMG。

通过行进立方体进行网格划分 [122]。在高分辨率情况下，与体素分辨率的立方成正比的浮点运算是无法忍受的。对象占据的网格通常仅由聚集在同一区域中的少量立方体组成，这意味着许多计算被浪费了。为了克服计算复杂度高的问题，IM-NET [65] 提出了一种更有效的采样方法，即对形状表面附近的更多点进行采样，而忽略远处的大多数点。在解决从点云生成网格的任务时，后续工作 [80]，[121] 侧重于判断点云的占用率而不是整个 3D 空间，这直接减少了浮点计算。与前者相比，这些基于网格基本单元预测的 IMG 方法可以端到端地生成网格。Yao [48] 提出了第一种使用分类模型生成网格的算法，该算法用于确定是否添加新顶点以及以何种方式添加新顶点。IER [79] 通过在输入点云上构建 k-最近邻图，提出了一组候选三角形面，其中利用神经网络过滤掉不正确的候选面。IER 的流程图如图 6 所示。Scan2Mesh [66] 和 REIN [83] 通过对边的存在进行分类来生成网格。PointTriNet [82] 迭代应用了两个神经网络：分类网络预测候选三角形是否应该出现在网格中，而建议网络则建议其他候选三角形。PointTriNet 的提议网络避免了预先定义候选面的需要，并消除了所有点必须从三角形网格顶点派生的假设。虽然 PointTriNet 的应用范围有所扩大，但生成的网格仍存在诸多问题，如非流形、孔多等。

基于等值面的网格生成

假设每个点
都有一个属性值，并且
表示空间 X 中的隐式函数。然后，由具有相等属性值的连续空间组成的曲面称为等值面，其定义为：

现有的基于等值面的 IMG 利用神经网络来拟合隐式函数并提取
。三角形网格通常通过行进立方体 [122]、行进四面体 [123]、泊松曲面重建 [124] 算法或神经网络 [58]、[92]、[101]、[107]、[117] 进行重建。根据所选隐函数的不同，这些 IMG 方法分为四类：径向基函数（RBF）[52]、占用场 [32]、[54]、[57]、[58]、[61]、[73]、[78]、[84]、[88]、[91]、[110]、[119]、[121]、有符号距离函数（SDF）[39]、[60]、[64]、[65]、[69]、[76]、[77]、[80]、[87]、[90]、[92]、[94]–[97]、[99]、[101]、[103]、[107]–[109]， [113]、[117]、[120] 和无符号距离函数（UDF）[74]、[86]、[89]、[100]。不同类型的隐式函数如图 7 所示。

图 7：不同类型的隐式函数 [100]。

基于等值面的 IMG 具有表示复杂几何形状和拓扑结构的优点，并且不限于预定义的分辨率。因此，基于等值面的 IMG 受到研究人员的青睐。2009 年，Wen et al.[52] 利用基于最小二乘径向基函数的神经网络来估计每个表面样本上的系数，并构造一个连续的隐式函数来表示 3D 表面。该网络还克服了传统 RBF 重建的数值失调和过拟合问题，并提供了一种利用较少样本重建模型的工具，使几何处理变得可行和实用。之后，Lun 等人。[54] 使用解码器网络将前景概率函数与占用场拟合，其定义如下：

最近，出现了许多基于占用率预测的作品。Liao 等 [58] 通过预测每个体素的占用概率，提出了可微的行进立方体。为了提高体素占用预测的计算和记忆效率，Mescheder 等人提出了占用网络 [61]。目前，已经提出了各种具有不同网络架构和训练策略的基于占用的方法，以不断提高效率、鲁棒性和准确性 [32]、[57]、[73]、[78]、[84]、[88]、[91]、[110]、[119]、[121]。另外两个常用的隐式函数是 SDF 和 UDF。Cao 等 [60] 介绍了一种级联的 3D 卷积网络架构，该架构以渐进式、从粗到细的方式从嘈杂和不完整的深度图中学习 SDF。Wang 等.[64] 提出了一个深度隐式表面网络，该网络通过预测底层 SDF 从 2D 图像生成高质量、细节丰富的 3D 网格。在这些方法中，利用神经辐射场（NeRF）的 IMG 方法在再现物体或场景的外观方面显示出有希望的结果 [120]，[125][126]。对于它们来说，NeRF 用于预测 SDF 或密度场。然后，可以使用行进立方体算法从 SDF 中提取网格。尽管神经内隐表征在 3D 重建中因其表现力和灵活性，神经隐式表示的本质会产生缓慢的推理时间，并且需要仔细初始化。为了解决这些问题，Peng 等人。[99] 使用可微分 PSR [124] 引入了可微点到网格层，该层通过隐式指示器字段将显式 3D 点表示与 3D 网格桥接起来，从而实现端到端优化。其流程图如图 8 所示。

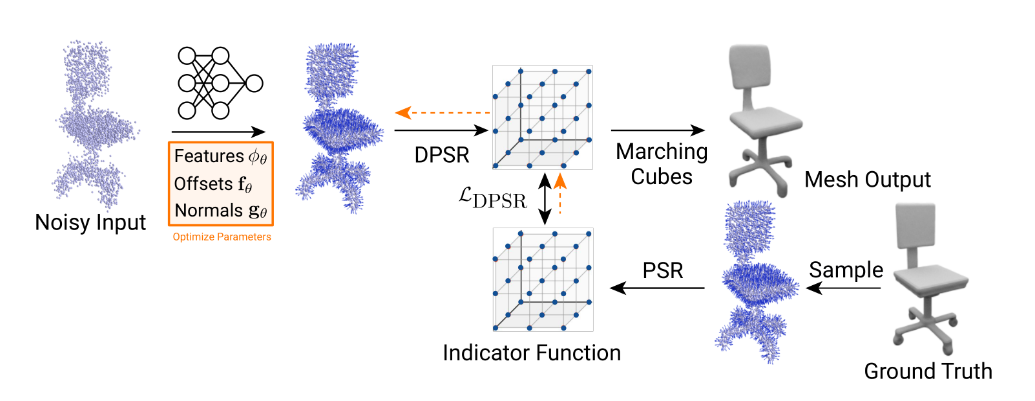
图 8： SAP [99]：一种基于等值面的 IMG 方法

Mon 等 [74] 介绍了一种与符号无关的学习方法，用于直接从原始和无符号几何数据中学习隐式形状表示。在文献 [86] 中，提出了神经距离场来预测给定稀疏点云的任意三维形状的无符号距离场。为了通过隐式表示估计局部几何，例如法线和切线平面，Venkatesh 等人。[89] 利用了一种称为最接近表面点表示的有效隐式表示，用于解决表面上的偏微分方程相关问题 [127]–[132]。为了处理高度稀疏的输入点云，NeeDrop [100] 引入了一种基于统计的自监督方法，直接从点云中估计占用函数。等值面方法系列有时受到其对噪声、异常值和非均匀采样的敏感性的限制。此外，在隐式方法中大规模求解方程可能非常耗时。分辨率与运行时间以及内存使用量之间存在三次或二次关系，这限制了其应用价值。

基于 Delaunay 三角测量的网格生成

Delaunay 三角测量 [133] 是一种广泛使用的网格重建技术，可以将点云连接成三角形网格。Delaunay 三角剖分具有许多优良的特性，例如最大化最小角度特性。无论从哪个区域构建 Delaunay 三角剖分，最终生成的三角形网格都是独一无二的。受 Delaunay 三角测量的启发，一些研究人员试图将其集成到 IMG 中，以生成高质量和流形网格 [43]–[46]，[49]，[98]，[104]，[106]。在这些方法中，早期作品 [43]–[45]，[49] 使用神经网络预测顶点的位置，然后使用 Delaunay 三角测量 [133] 生成高质量的网格。这些方法生成具有给定边界或粗网格的二维平面网格。然而，在应用中，经常需要解决三维表面问题。Alfonzetti [46] 利用 3D Delaunay 算法从 3D 点云生成四面体网格。Song 等 [93] 将分类模型与自适应 Delaunay 算法相结合，实现了室内外大场景的网格重构. Rakotosaona 等人。[104] 通过神经网络将一个 3D 点投影到 2D 参数空间中，使用 Delaunay 算法对 2D 平面点进行三角测量，然后通过逆向映射将点云拉回 3D 表面。算法流水线如图 9 所示。此外，为了实现端到端的可微三角测量, Rakotosaona 等人。[98] 提出了一种可微分加权的 Delaunay 三角剖分法。

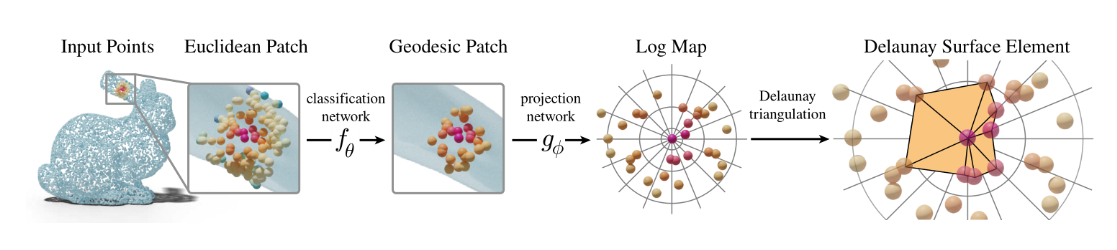
图 9： DSE [104]：基于 Delaunay 三角测量的 IMG

基于参数化的网格生成

如 [134] 所述，参数化是嵌入在 3D 中的曲面网格与称为参数空间的简单 2D 域之间的对应关系。通常，参数化应该是双射的，这是计算机图形学和几何处理中的一个经典问题，具有多种应用，例如网格生成、纹理映射和形状对应。考虑到网格生成在参数空间中的便利性，一些研究者尝试将参数化与机器学习模块相结合，然后发明了一系列基于参数化的 IMG 方法。根据参数化参与模式的不同，我们大致将其分为两类。第一类是基于几何图像的 IMG。作者通过传统的参数化方法 [135] 将表面映射到参数平面上，得到几何图像，利用深度学习模型对几何图像进行处理，然后将几何图像转换为网格。第二类是基于参数化学习的 IMG，它学习从参数空间到目标空间的映射。然后，通过传统或机器学习方法在参数空间中生成网格。对于第一类，Sinha 等 [55] 开发了一种创建几何图像的程序，该图像表示一类 3D 对象的形状表面。然后，作者利用这些几何图像通过开发深度残差网络的变体来生成特定类别的表面。Li 等.[63]， [118] 提出了预测生成对抗网络和预测补偿生成对抗网络来学习几何和法线图像的联合分布以生成网格。他们的目标是使用两个生成对抗网络（GAN）[136] 生成网格，并在面部网格生成方面取得了良好的性能。这种方法的优点是可以通过 2D 网格卷积直接处理 3D 对象。然而，角度和面积畸变往往被忽略。Surfnet [55] 通过使同一类的不同对象具有相同的几何图像，在一定程度上减少了区域畸变的影响。对于第二类主要思想是通过神经网络拟合从参数空间到对象空间的映射，反之亦然。早期的工作 [50] 通过拟合双变量函数将平面网格提升到表面。在文献 [51] 中，学习了从二维三角形晶格到三维空间中曲面的映射，以将参数空间中的网格提升到目标曲面。其他研究人员尝试将 3D 点云投影到 2D 平面上，在平面上生成网格，然后将其拉回。考虑到表面拓扑结构的复杂性和差异性，部分工作选择拟合局部同态映射 [26]、[56]、[67]、[75]、[98]、[104]、[105]。另一部分通过假定曲面类型 [53]、[102]、[111]、[115] 直接拟合全局映射。图 10 显示了一种局部参数学习方法 DST [98]，该方法将源分解为局部补丁，然后执行每个补丁网格划分。该方法采用参数化
（一种双射和分段可微映射）将 3D 曲面投影到 2D 参数空间中。然后，使用
提升 2D 顶点，在曲面上形成软 3D 三角测量。DST 的优点是保证生成的网格为 2-流形，限制是分区导致的边界伪影，这是所有局部参数化方法的共性问题。

图 10： DST [98]：一种基于参数化的 IMG 方法

基于前沿的网格生成

前沿方法是一种贪婪算法，它从边界到内部逐渐生成网格节点并递归执行。每个递归过程分为三个步骤：首先，从分割网格域和非网格域的生成段前端集中选择一个线段，其中所选段称为基段，因为它将构成创建新三角形元素的基础; 其次，将新的网格节点或已有的网格节点连接到基段，以生成新的三角形单元; 最后，更新生成线段 Front Set 和 Triangle 元素。受到经典前沿方法的吸引，一些研究人员试图将其与机器学习模块相结合，以设计新的实用算法。早期的前进前沿方法可以生成简单的网格，但它涉及许多低效的计算 [137]，[138]。Yao 等 [48] 将新的顶点位置预测和分类相结合，生成了四边形网格。RLQMG [116] 将前进前沿方法与强化学习相结合，分别通过状态表示和动作表示生成波前和新点。Lu 等 [114] 使用深度学习来学习前进的方向和步骤。这种方法的主要局限性是无法保证生成的网格的质量（例如，异常点太多）。此外，现有的基于前沿的先进方法只能生成平面网格。

基于生成类型的分类

根据输出网格基元的类型，我们将 IMG 分为三角形、四边形、混合多边形和四面体网格生成。这种分类使我们能够识别每种方法生成的网格类型，从而使用户能够选择最适合他们需求的内容。如表 1 所示，目前大多数 IMG 方法都生成三角形网格。这种趋势是合乎逻辑的，因为三角形网格仍然是流行的格式，并得到了丰富的工具和理论知识的支持。这一观察结果还强调，三角形网格划分以外的领域，如四边形网格划分和体积网格划分，是需要进一步探索的领域。

三角形网格生成

三角形网格可以说是最主要的曲面网格表示。它的受欢迎程度源于它的简单性、灵活性以及许多数据结构的存在，以实现高效的网格导航和操作。随着公开的三角形网格数据集的增加和深度学习技术的进一步发展，已经提出了许多方法来生成给定点云、图像或其他形式数据的三角形网格。值得注意的是，早在 1990 年代，智能三角网格生成算法就引起了研究人员的兴趣。这一时期的主要研究重点是密度自适应三角网格生成算法 [42]–[46]，[49]，其主要特点是在神经网络学习的密度函数的指导下，在初始粗网格上生成具有所需非均匀密度的三角形网格。然而，上述方法主要集中在平面网格上，很少考虑三维物体的表面网格生成。因此，为了提高算法适应真实输入的实用性，越来越多的研究人员致力于研究 3D 网格生成。Peng 等.[47] 探讨了神经网络在三角网格重建和 3D 对象表示中的可行性。虽然这种方法非常简单，但它通过预测 z 坐标实现了从 2D 到 3D 的提升。随着 3D 数据采集设备的快速发展，以 3D 数据为输入的三角形网格生成正在成为 IMG 的重要分支。三角形网格生成大致分为两种类型：（1）显式方法，直接从输入点恢复三角形网格，（2）隐式方法，旨在恢复体积函数，其零级集对曲面进行编码。对于前者，我们将点云视为简并网格（即两点之间没有连接关系的网格）。因此，需要选择顶点并预测正确的邻接关系。具体而言，Scan2mesh [66] 通过对点位置和连接关系的联合预测来生成三角形网格。但是，使用全连接图作为候选边集会使边信息变得多余。Daroya 等人。[83] 提出了 REIN，这是一个基于 RNN 的网络，通过顺序边缘预测生成具有不同数量顶点的网格。如第 3.1 节所述，一些基于模板变形的方法也等同于初始化点连接关系。对于后者，曲面三角形网格通常使用行进立方体 [122]、行进四面体 [123] 或泊松曲面重构 [124] 算法进行重构。但是，这些方法无法保持清晰的特征，并且不是端到端的。因此，一些研究人员探索了可微行进立方体算法来保持清晰的特征。Liao 等 [58] 展示了一种实现端到端训练的可微分替代方案。Liu 等人 [94] 提出了一种基于等值面的深度移动最小二乘法来生成三角形网格。Chen 等 [107] 重新设计了行进立方体算法，并构建了一些镶嵌模板，可以更好地保留锐利的特征。Chen 等.[117] 改进了双轮廓算法 [139]，最终允许端到端训练。另一个分支是基于 2D 图像或特征的三角形网格生成方法，它比基于 3D 数据的方法更模糊，并且在辅助网格生成之前需要更高的鲁棒性。遮挡信息的重建和深度信息的估计变得尤为重要。一些基于变形的方法和基于参数化的方法已成为解决上述情况的主流方法。对于前者，图像被认为是指导模板变形的信息。典型的代表 Pixel2Mesh 系列 [10]、[15]、[17]、[31]。对于后者，我们将 2D 特征理解为 3D 对象表面的参数化。基于几何图像的 [55]，[118] 方法值得注意。

四边形网格生成

由于四边形网格具有吸引人的张量积性质和平滑表面近似，因此在许多应用中，四边形网格划分技术通常比三角形网格更受欢迎，例如纹理、有限元仿真和 B 样条拟合。为了利用深度学习强大的表示和泛化能力，一些研究人员还尝试将深度学习与四边形网格生成相结合，并获得了良好的解决方案 [26]、[29]、[42]、[48]、[105]、[111]、[115]、[116].遵循传统的分类方法，我们将基于深度学习的四边形网格生成分为直接 [29]、[42]、[48]、[115]、[116] 和间接 [26]、[105]、[111] 方法，根据是否需要中间模型表示。在这些直接 IMG 方法中，Ahn 等 [42] 提出了一种自组织神经网络，该神经网络通过变形初始网格来实现自动非均匀密度四边形网格生成。姚明等.[48] 提出了一种基于人工神经网络的单元提取方法，用于自动生成有限元四边形网格。作者设计了合理的节点插入类型，然后利用神经网络预测节点位置和插入类型。网格边界通过多次更新迭代不断推进。Pedone 等 [29] 生成了一个小型变形矩形网格的数据库。Chen 等 [115] 介绍了一种以无监督方式生成结构化网格的微分方法。该方法以边界曲线为输入，采用精心设计的神经网络来分析潜在的网格划分规则，并输出具有所需单元数的网格。为了克服传统方法在实现高质量网格和计算复杂度之间取得平衡的困难，Pan 等 [116] 提出了一种基于强化学习的自动四边形网格生成方法。不幸的是，所有这些方法都只能处理简单的平面或曲面。对于间接方法，Smirnov 等 [26] 学习了一种特殊的形状表示：由 Coons 面片组成的可变形参数模板。给定光栅图像，首先，系统推断一组参数化表面，以实现 3D 输入。然后，使用模板生成四边形网格。Deng 等 [111] 提出了 Sketch2PQ 系统，该系统使用描边线、深度样本以及从草图中诱导的可见和遮挡区域蒙版作为输入。首先，Sketch2PQ 计算方向场和 B 样条曲面作为中间模型表示。然后，通过几何优化从 B 样条曲面和 CDF 中提取四边形网格。另一个有趣的工作是 LDFQ [105]，它从三角形网格中学习交叉场以生成四边形网格。他们的网络可以推断出类似于四边形对齐的帧场。这种丰富的指导信息能够保证生成正确和高质量的四边形网格。LDFQ 的流水线如图 11 所示。

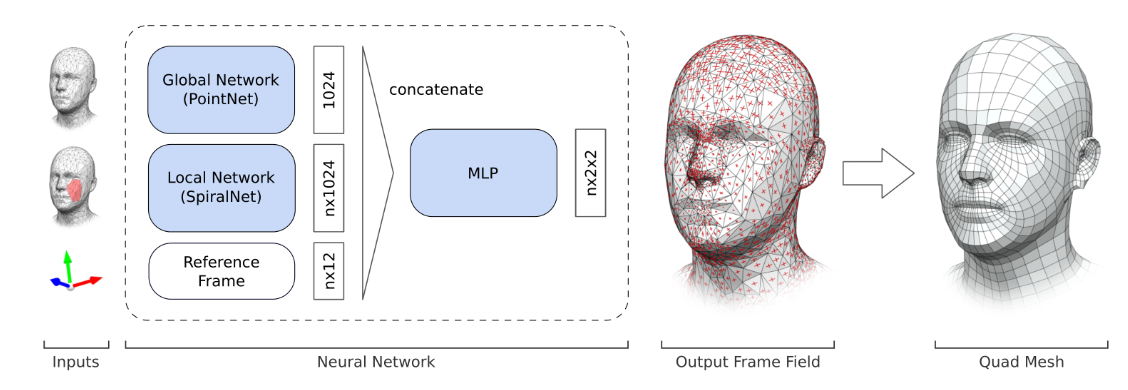
图 11：LDFQ [105]：一种用于四边形网格的 IMG 方法。

混合多边形网格生成

在实际应用中，由于各种非理想条件，往往不可能只生成一个基本面。因此，一些研究人员出于主动或被动的意图设计了混合网格生成算法。然而，由于其应用的局限性，以混合网格为生成目标的 IMG 类型屈指可数。在我们检索的文献中，只有 BP-ANN [114]、AnalyticMesh [101] 和 PolyGen [70] 属于这一类。BP-ANN 通过推进前沿方法生成各向异性的四边形和各向同性三角形网格，提高了混合网格生成的自动化水平和效率。AnalyticMesh 在分析单元之间移动，以恢复由隐式表面网络捕获的闭合分段平面表面的精确网格。该算法适用于更高级的 MLP 架构，包括具有快捷连接和最大池化操作的架构，这些架构支持一组更丰富的架构设计，用于学习和精确划分复杂曲面形状的网格。Polygen 更紧凑地表示具有不同多边形的对象表面。

四面体网格生成

四面体网格生成是网格生成的一个重要分支。与曲面网格不同，四面体网格生成同时划分了物体的表面和内部。四面体网格在数值模拟中起着不可替代的作用，因此受到了众多研究者的关注。然而，由于问题的复杂性和基础理论的不完备性，智能四面体网格生成仍然缺乏。在我们选择的文献中，四面体网格生成过程已被深度学习模块部分 [46] 或完全 [81] 取代。在 [46] 中，Alfonzetti 等人提出了一种用于四面体网格的神经网络生成器。从初始的适度粗网格开始，生成器通过节点概率密度函数将网格增长到用户指定的节点数。DefTet [81] 针对顶点放置和占用进行了优化，并且相对于标准 3D 重建损失函数是可微分的。与以前的工作相比，DefTet 具有多项优势，并且可以输出具有任意拓扑结构的形状，使用四面体的占用来区分对象的内部和外部。DefTet 还通过变形这些四面体中的三角形面来表示局部几何细节，以更好地与物体表面对齐，从而以比现有体积方法低得多的内存占用实现高保真重建。DefTet 接受点云或图像作为输入数据来生成网格。DefTet 的算法流程如图 12 所示。

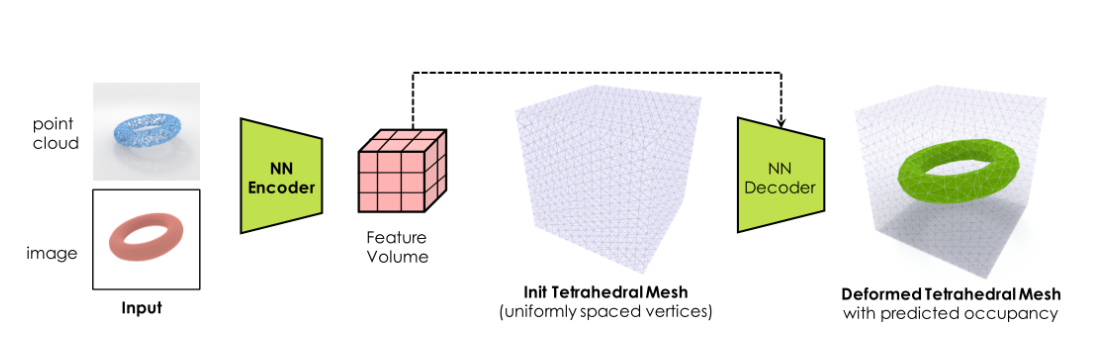
图 12：DefTet [81]：四面体网格的 IMG 方法。

基于输入数据类型的分类

根据适用的输入数据类型，我们将 IMG 分为基于点云、基于图像、基于体素、基于网格、基于边界或草图以及基于潜在变量的网格生成等类别。这种分类使我们能够识别每种方法所需的输入数据类型，从而使用户能够选择与其特定数据类型或用例最相关的方法。如表 1 所示，大多数现有的 IMG 方法从图像或点云生成网格，这可能是由于与其他方法相比，获取这些类型的数据相对容易。后续小节将提供更多详细信息。

基于点云的网格生成

点云作为 3D 数据的主要表示形式，在自动驾驶、AR 等领域得到了广泛的应用，与 RGB 图像相比，点云自然具有深度信息，不受环境光照条件的影响。从点云重建网格是计算机图形学中一个长期存在的问题。最近，已经开发了各种方法来重建一系列应用的形状 [3]。这些方法分为两类：

点位置和连接关系的直接估计（如图 13 所示）
基于等值面的隐式表面重建。

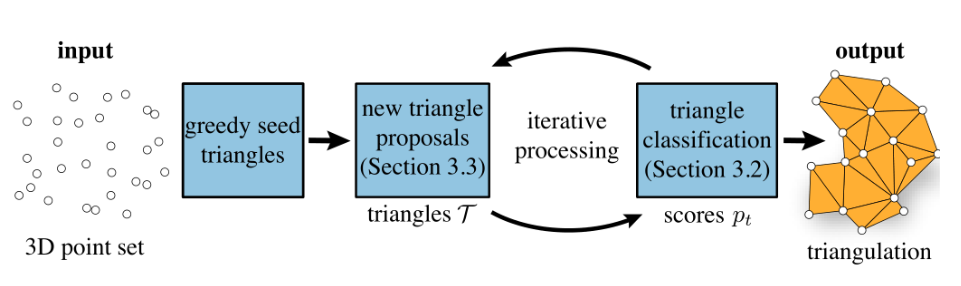
图 13：PointTriNet [82]：一种基于点云的 IMG 方法。

第 4.1 节说明了这种划分。接下来，我们从两个方面介绍这些方法：

基于点云的网格生成的挑战，
为应对这些挑战而提出的可学习先验和相关方法。

基于点云的 IMG 方法的挑战来自数据和任务目标。对于数据方面，虽然点云是易于访问的 3D 数据，但它们通常稀疏、嘈杂甚至不完整。为了应对这些挑战，研究人员提出了多种方法 [39]、[50]、[75]、[83]、[97]、[100]、[110]、[113]。Li 等 [50] 率先考虑了基于神经网络从不完全点云生成网格的问题。Badki 等 [75] 通过学习局部几何先验来处理稀疏或嘈杂的点云，同时确保全局几何的一致性。Boulch 等 [100] 和 Ma 等 [39]，[113] 通过将查询 3D 位置拉到表面上的最近点，从稀疏的点云中重建了高精度网格。对于任务目标，大场景网格重构和流形网格生成是该领域的重点。大场景网格重建 [77]、[91]、[93]、[95]、[106]、[110] 等项目取得了较大进展，但距离实际应用还有很长的路要走。流形网格生成 [98]、[99]、[104]、[107]、[117] 主要通过结合 Delaunay 三角测量或行进立方体算法来实现。例如，Chen 等 [107] 提出了第一个基于行进立方体的方法，能够恢复尖锐的几何特征。Rakotosaona 等 [104] 利用二维 Delaunay 三角剖分的特性来构建三维网格。

基于图像的网格生成

基于图像的网格生成的目标是从一个或多个 2D 图像中推断对象或场景的 3D 网格。仅从 2D 图像中恢复丢失的尺寸是一个不合理的问题，也是许多应用的基础，例如机器人导航、3D 建模和动画、工业控制和医疗诊断。深度学习技术的快速发展，更重要的是，越来越多的公共数据集，加速了这一子领域的发展。尽管是最近才出现的，但这些方法在各种任务上都显示出令人兴奋和有希望的结果 [4]。基于图像的方法面临的直接困难之一是如何维护和表示物体的几何和拓扑信息。Sinha 等 [55] 构建网络来学习几何图像，以图像为输入以生成 3D 网格。形状的几何信息通过参数化学习来保留。Wang 等 [10] 使用基于变形的方法来恢复几何形状和拓扑结构。之后，出现了许多基于变形的方法 [15]，[17]–[20]。Wen 等人. [15] 使用多个图像来构建几何细节，如 14 所示。Tong 等 [18] 使用特定的模板来提供更多的几何细节。虽然有很多优秀的作品，但泛化仍然是这些基于变形的 IMG 技术的弱点。其他研究人员已将注意力转向纹理网格的重建。尽管 RGB 图像提供了一些纹理信息，但这项任务比单纯生成网格更具挑战性。Henderson 等人。[23] 专注于从 2D 图像生成 3D 纹理网格的问题。Munkberg 等 [108] 同时从多视图图像观测中优化了拓扑、材料和照明。诚然，在探索 3D 网格纹理和 2D 图像之间的对应关系时，IMG 的可解释性得到了增强。此外，基于图像序列和视频的网格生成也值得关注 [24]、[28]、[29]、[33]、[88]、[90]。

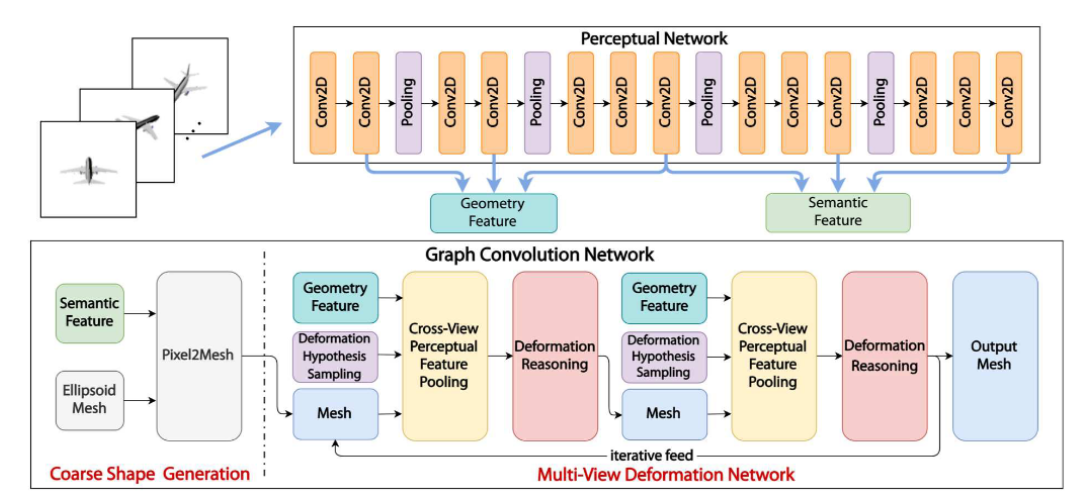
图 14：Pixel2Mesh++ [15]：一种基于图像的 IMG 方法。

基于体素的网格生成

体素是一种数据结构，它使用固定大小的立方体作为表示 3D 对象的最小单位。体素是存储体积数据、提供密度、不透明度、法线和其他信息的传统方法。体素格网的索引提供位置信息。体素建模的主要缺点是体素的存储和计算需要大量的内存资源。与点云类似，一类基于体素的方法使用占用率和等值面来隐式生成网格。Mescheder 等 [61] 使用占用网络进行 3D 分辨率增强，以更好地重建物体。Voxel2Mesh [40] 利用网络从体素化的 MRI 脑图像和 CT 肝脏扫描中提取特征，并依靠变形网络获得目标物体的三角形网格。Peng 等.[77] 将卷积编码器与隐式占用解码器相结合，实现了对象和 3D 场景的详细重建。作者将输入编码为 2D 或 3D 体素网格，这些网格使用卷积网络进行处理，然后通过全连接的网络解码为占用概率。DMTet [92] 是一个深度 3D 条件生成模型，可以使用简单的用户指南（如粗体素）合成高分辨率的 3D 形状。该模型通过可微的行进四面体层结合了隐式和显式 3D 表示的优点。这种组合允许使用重建和对抗损失来联合优化表面几何形状和拓扑结构，以及生成细分层次结构。作为等值面提取的中间产物，体素化距离场也经常被用作生成网格的输入 [66]，[107]，[117] Scan2Mesh [66] 将体素化截断符号距离场（TSDF）作为输入。其框架如图 15 所示。Scan2Mesh 由两个主要组件组成：首先，3D 卷积和图神经网络用于联合预测顶点位置和边缘连通性。第二，使用图神经网络预测最终的网格面结构。NMC [107] 使用有符号距离场作为输入，然后进行训练以重建隐式场的零等值面，同时保留锐边和平滑曲线等几何特征。NMC 的主要局限性在于它对旋转敏感，无法避免网格的自交。NDC [117] 是一种基于双轮廓的数据驱动的网格重建方法。可以训练 NDC 从二元体素网格、有符号或无符号距离场或点云生成网格，并且可以在输入表示图纸或部分曲面的情况下生成开放曲面。

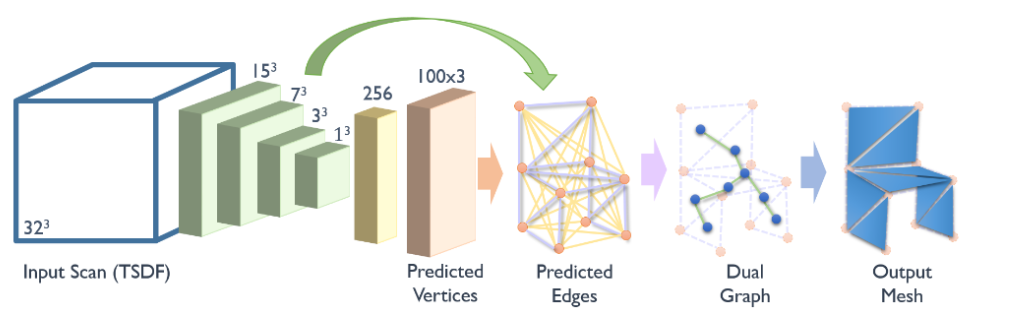
图 15： Scan2Mesh [66]：一种基于体素的 IMG 方法。

基于网格的网格生成

在 IMG 中，基于网格的输入主要用于两个任务：网格优化 [44]–[46]、[49]、[112] 和四边形网格生成 [105]。早期基于深度学习的网格生成倾向于将粗网格作为输入，并通过神经网络对其进行细化以满足对象的几何和拓扑信息。在 [44] 中，Alfonzetti 提出了一种自动网格生成器，即 Let-It-Grow 神经网络。该算法从具有少量顶点的三角形的粗略网格开始，增加顶点数，直到达到用户选择的值。顶点增长由预定义的概率密度函数驱动。在 Alfonzetti 的后续工作 [45]，[46]，[49] 中，他遵循了 [44] 中的想法，并提出了不同的解决方案。Liu 等 [72] 提出了一种新的数据驱动的从粗到细几何建模的框架。Hahner 等人。[112] 提出了一种自动编码器，可以处理不同大小和拓扑结构的半规则网格。该算法可以高质量地重建网格，并泛化到看不见的时间序列的动态。Dielen 等人。[105] 提出了一种神经网络，可以从非结构化三角形网格推断帧场。然后，通过现有的基于参数化的四边形方法从框架场重建四边形网格。

基于边界或草图的网格生成

与点云或图像相比，边界和草图是两种更简洁、更易于获取的数据。因此，边界和草图是网格生成任务的常用输入数据形式。边界定义了网格覆盖的区域，给出了网格的初始位置和增长方向，并且是推进基于前端的网格生成方法的常见输入。草图描绘了 3D 形状的丰富几何特征，例如轮廓、遮挡和暗示轮廓、山脊和山谷以及影线，从而为网格生成提供了一种简洁直观的方法。在我们收集的 IMG 中，基于边界的网格生成方法 [21]、[42]、[43]、[48]、[114]–[116] 通常用于 2D 平面网格，而基于草图的方法 [9]、[26]、[41]、[54]、[57]、[78]、[111] 通常用于 3D 物体表面网格。对于基于边界的 IMG，大多数方法通过前进前沿技术 [48]，[114]，[116] 或通过在给定初始边界条件下求解偏微分方程 [21]，[115] 来生成二维网格。此外，A. Chang-Hoi et al. [42] 和 D. Lowther et al [43] 通过生成网格变形和点预测。草图可以被认为是一个非常稀疏的图像。因此，需要额外的信息（例如，深度信息）或全局和局部约束。Lun 等人。[54] 基于草图的生成分为两个阶段：首先，从多视图草图生成深度和法线图像，其次，从深度和法线图像生成表面。Li 等.[57] 使用 CNN 来推断表示表面的深度和法线贴图，中间层对曲率方向场进行建模并生成置信度图以提高鲁棒性。邓等.[111] 使用可见和遮挡边界、等高线和特征线以及一些深度样本生成四边形网格。边界和特征线共同决定了网格的样式，如 16 所示。

图 16 Sketch2PQ [111]：基于草图的四边形网格 IMG。

基于潜在变量的网格生成

GANs 和变分自编码器（VAEs）[140] 作为两大主流的生成模型，自然而然地在 IMG 中发挥了作用。众所周知，这两种模型都可以在训练后直接从潜在变量（随机噪声）生成图像。受到图像生成成功的启发，一些研究人员进行了基于 GAN 和 VAE 的网格生成研究。考虑到模型训练后生成网格只需要潜在空间的潜在变量，该文将该方法归类为基于潜在变量的网格生成 [59]、[62]、[63]、[69]、[85]、[118]。具体来说，Li et al.[63]， [118] 使用 GAN 模型从潜在变量生成几何和法线图像，然后通过后处理生成网格。其他一些研究 [59]，[62]，[85] 选择了 VAE 模型来重建、变形或插值网格。Pq-Net [69] 使用条件变分自动编码器实现了零件的序列生成。

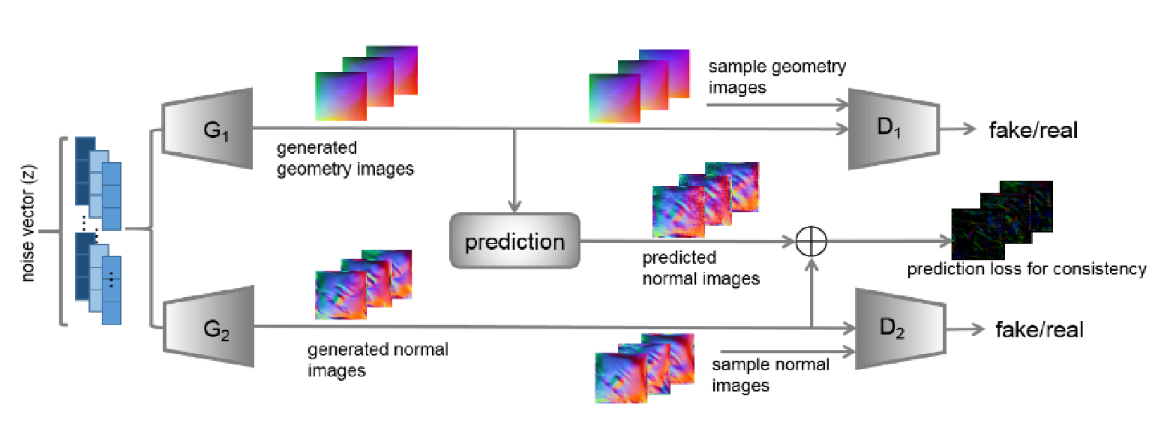
图 17： PGAN [63]：一种基于潜在变量的 IMG 方法。

评估

一般来说，各种 IMG 的评估方法分为两大类：定性和定量。我们的定性分析侧重于所有 IMG 方法的内容视角，包括针对性挑战、优势、局限性和平均每月引用次数。另一方面定量评估通常强调特定指标，例如时间复杂度和网格质量。在本节中，我们根据从所有选定方法中提取的内容进行彻底而全面的定性分析。然而，由于各种 IMG 方法的目标任务和数据集差异很大，它们采用的指标差异很大。因此，我们避免对所有 IMG 方法进行定量比较，而是提供常用指标列表。

内容评估

我们从综述的论文中提取了所提算法的主要挑战、优势和局限性，并按时间顺序在表 2 中进行了排序。关键挑战往往是论文的目标，并在一定程度上体现了它的价值。优势往往体现在对挑战的有效解决方案上。这些局限性指出了该算法的不足，并为未来的研究指明了方向。在具体应用中，这三个方面也为我们提供了选择合适的算法的指导。在优点和局限性的总结中，我们没有使用诸如更高的准确性、更快的速度或更少的内存需求等短语。随着 IMG 技术的发展，原文中声称的优势往往难以为继。因此，我们尝试根据任务目标和应用场景给出更客观的评价。此外，我们计算并展示了每篇论文的平均月度引用次数（AMC），这在一定程度上反映了相应工作的影响力。

指标

在我们早期的定量分析尝试中，我们经历了复杂而艰巨的数据整理和分析。虽然我们最终失败了，但我们也意外地发现，缺乏基准测试是阻碍 IMG 发展的挑战。这里的基准测试包括统一的测试数据和指标。对于定量分析，大多数方法都会创建自己的测试数据。即使数据集相同，测试数据也会因预处理不同而有所不同。而且，指标选择的差异也直接导致了量化比较的无法进行。由于上述无法克服的问题，我们放弃了对现有 IMG 方法进行全面定量比较的尝试。接下来，我们列出并解释 IMG 中常用的指标，以便读者了解该领域综合比较的挑战。根据评估的指标，我们将这些指标分为错误和特征保留指标、拓扑指标和感知指标。

错误和特征保留指标
1. 在 IMG 中，倒角距离（CD）[141] 是衡量重建网格 M 与目标曲面 M 之间误差的最普遍指标。CD 定义为两个点云之间最小距离的平均值。点的坐标范围、点的密度和距离范数的定义将直接影响 CD 的值。无论坐标是否归一化、网格上的采样点数量以及距离是否为 Lor Lnorm，都会产生不同的 CD 值，从而无法进行比较分析。F 分数 [10] 定义为精确率和召回率的谐波平均值，其中召回率是 M 上与 M 相距一定距离内的点的分数，精度是 M 上与 M 相距一定距离内的点的分数。F 分数主要捕捉重大错误，忽略对视觉伪影有重大影响的小错误。然而，不同的阈值和距离选择策略直接导致不同的 F 分数值。正态一致性评分 [61] 衡量的是 3D 模型曲面法线的一致性，即相邻面的法线应该是平滑连续的，而不是明显不连续或不一致的。测试数据必须包含精确的法向量，并且涉及复杂的投影，因此应用场景有限。
拓扑指标
1. 水密性和流形性是两个拓扑指标。水密性 [82] 表示正好具有两个入射三角形的边的百分比，流形性 [82] 表示具有一个或两个入射三角形的边的百分比。这两个指标从拓扑的角度测量网格，但忽略了目标表面的几何形状和特征。
感知指标
1. 正如 [65]，[142] 所指出的，诸如均方误差和 CD 之类的指标并不能解释物体表面的视觉质量。对于视觉感知，形状中的低频误差不如高频误差明显。为了克服传统质量指标的缺点，出现了基于视觉相似度或感知质量的深度学习测量方法 [143]–[149]。然而，这些模型的泛化性和适用性有待提高，因此很少用于定量比较分析。

如上所述，我们不能用现有的结果来比较所有这些 IMG 方法，也不能直接通过实验来比较它们。对这些 IMG 方法进行比较分析是非常具有挑战性的。然而，为了方便研究人员选择自己感兴趣的论文，我们在补充材料和项目库中提供了一些不完善的定性比较结果和比较关系图。

外部资源

常见数据集

数据是 IMG 发展的基石。输入的多样性突显了 IMG 方法所采用数据集的多样性。遗憾的是，目前不存在体积网格的公共数据集。因此，我们在这里的重点仅限于三角形和四边形网格的常用数据集。

三角网格
1. 这些常用的三角形网格数据集包括 Princeton ModelNet、ShapeNet [150]、TOSCA [151]、COSEG [152]、Berger [153] 和 Williams [67] 的表面重建基准、Thingi10K [154]、D-FAUST [155]、Famous [80] 和 CAD 数据集 ABC [156]; 用于单图像 3D 形状建模的数据集：Pix3d [157]; 面部表情数据集：COMA [59] 和 MeIn3D [158]; 人体形状数据集：MGN [11] 和 MultiHuman [159]; 具有真实纹理的服装身体网格：RenderPeople [160]、Axyz [161] 和 Digit Wardrobe [11]; 和室内场景数据集：ScanNet [162]、Scenenet [163]、Matterport3d [164]、和合成室 [77]。最常用的两个数据集是 ShapeNet 和 ModelNet。ShapeNet 包含来自多种语义类别的 3D 模型，并将它们组织在 Word-Net 分类法下。ShapeNet 已对超过 3,000,000 个 3D 模型进行了索引，其中 220,000 个模型分为 3,135 个类别。ModelNet 有 662 个对象类别和 127915 个 CAD 模型。它包含三个子集：具有 10 个类别的 Modelnet10; Modelnet40 有 40 个类别; 和 Aligned40 与 40 类对齐的 3D 模型。
四边形网格
1. 常用的四边形网格数据集包括 QuadWild [165]; 具有真实纹理的服装身体网格：RenderPeople [160]、Axyz [161]。值得注意的是，四边形网格数据集不够充分，这也在很大程度上阻碍了该领域的发展。

常用的先验

在 IMG 中，常用的基础先验包括平滑的 ness（smooth-ness）、基元（primitives）、分布（distribution）、用户驱动（user-driven）、方向（orientation）、可见性（visibility）和规律性（regularity priors.）先验。在缺乏监督信息的情况下，这些先验为模型优化提供了有效的指导。下面，我们将详细介绍它们。表面光滑度先验约束重构曲面以满足一定程度的光滑度。最一般的形式是局部光滑度，例如拉普拉斯光滑约束，它通常作为目标函数的常规项 [10]、[14]–[17]、[20]、[25]、[40]、[81]。几何正则化 [111]，[113] 试图将点拉到它们的邻居。在平滑先验约束下，模型通常会滤除噪声，但也会丢失一些高频细节。几何基元先验假设场景几何可以用一组紧凑的简单几何形状来解释，即平面、盒子、球体和圆柱体。方向先验是传统网格生成中的重要先验，适用于基于深度学习的网格生成任务。在基于距离场生成物体表面时，正态一致性先验保证了方向的一致性 [74]。可见性先验对重建场景的外部空间以及它如何为对抗噪声、不均匀采样和缺失数据提供线索。具体来说，Deng et al. 在 Sketch2PQ [111] 中，通过深度-法线兼容性项和深度样本项使用可见性。Sulzer 等 [106] 巧妙地利用了从相机位置获得的能见度信息，并制作了水密网格。Song 等人。[93] 明确地采用深度补全来预测 3D 点的可见性。全局规律性先验利用了许多形状在其更高层次的构图中具有一定程度的规律性的概念。规律性是指整体与部分的关系 [69]，[76]。同一种对象由相似的基本子部分以相似的排列方式组成。例如，汽车由车轮、底盘和盖板从下到上组成。此外，对称性也是一种常见的规律性。

基于网格的经典学习架构

随着深度学习方法在计算机视觉中的成功，许多神经网络模型被引入到使用体积网格 [68]、[166]–[169] 和点云 [170]–[176] 进行三维形状表示。然而由于网格数据的复杂性和不规则性，只有少数神经网络同时使用几何和拓扑信息作为输入 [177]–[180]。MeshCNN [177] 是一种专为三角形网格设计的卷积神经网络，定义了以边缘为中心的卷积和池化操作。在边及其入射三角形的四条边上应用卷积，并通过保留曲面拓扑的边折叠操作应用池化。这些操作有助于直接分析原生形式的网格。MeshNet [178] 定义了三角形网格的面心卷积和池化操作。为了综合几何信息和拓扑信息，该网络提供了一个有效的数据预处理和网络框架。PD-MeshNet [179] 利用 3D 网格的边缘和面的特征作为输入，并使用注意力机制动态聚合它们。Singh [180] 设计了表面相关块，可以捕获不同尺度的局部特征。虽然上述网络模型中只有少数能够同时处理几何和拓扑结构，但在网格分析和特征表示的研究中已经涌现出许多优秀的工作。Masci 等 [181] 提出了利用网状连通性结构的卷积。从那时起，几种方法解决了网格结构和采样率的不规则性，提出了诸如对每个顶点的邻域进行均匀采样或通过光谱分解实现规则性等想法 [182]–[186]。最近，结合学习到的热扩散操作，DiffusionNet [187] 提供了跨表面几何表示的统一视角。另一条工作线试图理解网格的结构和连通性 [38]，[85]，[185]。例如，作者在与顶点相关的点特征上实现了卷积层，例如在 EdgeConv [174] 中。通过结合邻域或边缘信息，这些方法可以更好地综合表示网格表面的几何和拓扑信息。

讨论与结论

IMG 显著增强了传统网格生成技术的通用性、鲁棒性和实用性。然而，它也有其自身的一系列挑战：处理非理想数据、算法实用性和复杂的对象生成。非理想数据挑战需要处理缺乏 3D 信息的 2D 图像、稀疏和不均匀的点云、被遮挡或不完整的点云、嘈杂的数据和大规模输入数据。算法实用性存在一些障碍，例如确保广泛的泛化、实现高计算效率、保持低内存要求、对非理想输入表现出鲁棒性以及保证端到端的可微性。为复杂对象生成网格的挑战与复杂的对象或场景有关。这包括为大型动态场景创建网格、高密度细节、基于纹理的网格、溅水网格、非均匀密度网格和结构化网格。

公开提议摘要

在这篇综述中，我们强调了所选文章中发现的局限性。这些局限性不仅代表了 IMG 领域的挑战，同时也有助于确定未来潜在的研究方向。我们认识到的主要挑战如下：

泛化：
1. 泛化意味着算法处理训练期间未观察到的对象的能力 - 是证明算法实际效用的关键方面。缺乏泛化是当前 IMG 方法的一个普遍问题，特别是那些使用基于变形的网格生成技术的方法。这些方法通常会生成特定于特定对象类型或拓扑的网格，从而限制了其更广泛的适用性。
可解释性：
1. IMG 的可解释性至关重要，尤其是在航空航天工业中。我们建议将 IMG 与基本的数学和物理模型融合在一起，Zheng 等 [188] 和 Lei 等的研究证明了这一点。[189]，不仅可以有效地控制模型优化，还可以增强模型的可解释性。然而，到目前为止，还没有研究直接解决这一特定问题。
缺乏基准
1. 如第 6.2 节所述，对所有这些 IMG 方法进行全面的比较分析会带来重大挑战。缺乏标准化的测试程序，加上测试数据和指标的差异，严重阻碍了 IMG 的发展。因此，制定基准标准将大大加快 IMG 的进展。
水密和流形：
1. 在许多计算机图形应用中经常需要水密和流形网格。然而，目前基于单元分类的 IMG 方法无法生成水密或流形网格。在尝试从头开始生成网格时，这些方法会忽略某些局部约束。此外，由于水密和流形网格的离散性，它们无法提供模型优化所必需的梯度。
结构化网格：
1. 结构化网格具有非结构化网格无法比拟的诸多优势，包括高效的存储和访问。不幸的是，由于其固有的复杂性，MGNet [115] 是目前唯一考虑结构化网格生成的 IMG 方法。因此，探索能够处理真实世界对象的更实用的结构化或半结构化 IMG 算法至关重要。此外，四边形和体积网格数据集明显稀缺，这阻碍了 IMG 在结构化四边形网格和体积网格生成领域的发展。在这些领域创建开源数据集可以大大加快 IMG 在结构化网格环境中的开发。
纹理网格：纹理网格是 3D 对象中备受追捧的表示形式，广泛应用于工业设计和数字娱乐等众多领域。现有的 IMG 研究主要集中在重建几何和拓扑结构的挑战上。相比之下，只有少数研究集中在纹理网格的生成上 [23]，[108]，[190]。此外，纹理网格的生成无疑增强了模型的可解释性，使其成为 IMG 领域未来探索的重要领域。
大型或动态场景网格生成：
1. 场景网格生成在自动驾驶、室内机器人、混合现实等多个领域具有巨大潜力。要使 IMG 方法在实际应用中真正发挥作用，必须解决几个关键特性。首先，需要算法的实时功能。其次，该算法应该能够对没有观测值的区域做出合理的预测。此外，系统应展示可伸缩性以适应大型场景。最后，对嘈杂或不完整观测的鲁棒性至关重要。然而，现有的方法 [13]、[28]、[73]、[90]、[91]、[93]、[95]、[110]、[119] 不能同时满足这些标准，导致场景网格往往过于平滑和缺乏细节。

结论

在本文中，我们对智能网格生成（IMG）方法进行了系统而全面的回顾，重点介绍了核心技术、应用范围、学习目标、数据类型、目标挑战、优势和局限性。我们仔细研究了 113 篇研究论文，进行了详细的分析和数据提取。我们的主要提取点包括 1）已解决的挑战，2）基本概念、应用范围、优点和缺点，3）输入数据类型、输出网格的性质和网格质量，以及 4）未来研究的潜在方向。文章根据其技术、单元元素和适用的数据类型进行分类。虽然近年来 IMG 取得了长足的进步，但我们也发现了许多问题和挑战，为该领域未来的探索和研究铺平了道路。据我们所知，这是对现有 IMG 方法的最新和最全面的调查。本调查为 IMG 领域的学者提供了全面的视角和广泛的研究资源。但是，值得注意的是，我们的评论有一定的局限性。具体来说，我们的重点完全放在 IMG 上; 非机器学习网格生成方法超出了我们的范围。因此，许多关于传统网格生成的有价值的论文没有被收录。此外，尽管应用了系统的文献综述方法和人工检索以确保全面纳入，但由于现有文献数量庞大，在初始选择中可能忽略了相关论文。

引用

[1] J. P. Slotnick, A. Khodadoust, J. Alonso, D. Darmofal, W. Gropp,E. Lurie, and D. J. Mavriplis, “Cfd vision 2030 study: a path torevolutionary computational aerosciences,” Tech. Rep., 2014.
[2] S. Keele, “Guidelines for performing systematic literature reviews in software engineering,” 2007.
[3] M. Berger, A. Tagliasacchi, L. M. Seversky, P. Alliez, G. Guennebaud, J. A. Levine, A. Sharf, and C. T. Silva, “A surveyof surface reconstruction from point clouds,” in Comput GraphForum, vol. 36, no. 1, 2017, pp. 301–329.
[4] X.-F. Han, H. Laga, and M. Bennamoun, “Image-based 3d objectreconstruction: State-of-the-art and trends in the deep learningera,” IEEE TPAMI, vol. 43, no. 5, pp. 1578–1604, 2019.
[5] D. Khan, A. Plopski, Y. Fujimoto, M. Kanbara, G. Jabeen, Y. J.Zhang, X. Zhang, and H. Kato, “Surface remeshing: A systematic literature review of methods and research directions,” IEEETVCG, vol. 28, no. 3, pp. 1680–1713, 2020.18
[6] Y.-P. Xiao, Y.-K. Lai, F.-L. Zhang, C. Li, and L. Gao, “A surveyon deep geometry learning: From a representation perspective,”Comput Vis Media, vol. 6, no. 2, p. 8, 2020.
[7] W. Nianhua, L. Peng, C. Xinghua, and Z. Laiping, “Preliminaryinvestigation on unstructured mesh generation technique basedon advancing front method and machine learning methods,” J.Theor. Appl. Mech., vol. 53, no. 3, pp. 740–751, 2021.
[8] R. Daneˇrek, E. Dibra, C. ˇ Oztireli, R. Ziegler, and M. Gross, ¨“DeepGarment : 3D Garment Shape Estimation from a SingleImage,” Comput Graph Forum, vol. 36, pp. 269–280, May 2017.
[9] X. Han, C. Gao, and Y. Yu, “Deepsketch2face: a deep learningbased sketching system for 3d face and caricature modeling,”ACM TOG, vol. 36, no. 4, pp. 1–12, 2017.
[10] N. Wang, Y. Zhang, Z. Li, Y. Fu, W. Liu, and Y.-G. Jiang,“Pixel2mesh: Generating 3d mesh models from single rgb images,” in ECCV, 2018, pp. 52–67.
[11] B. L. Bhatnagar, G. Tiwari, C. Theobalt, and G. Pons-Moll, “Multigarment net: Learning to dress 3d people from images,” in ICCV,2019, pp. 5420–5430.
[12] J. Pan, X. Han, W. Chen, J. Tang, and K. Jia, “Deep meshreconstruction from single rgb images via topology modificationnetworks,” in ICCV, 2019, pp. 9964–9973.
[13] A. Venkat, C. Patel, Y. Agrawal, and A. Sharma, “HumanMeshNet: Polygonal Mesh Recovery of Humans,” in ICCVW, 2019, pp.2178–2187.
[14] G. Gkioxari, J. Johnson, and J. Malik, “Mesh R-CNN,” in ICCV,2019, pp. 9784–9794.
[15] C. Wen, Y. Zhang, Z. Li, and Y. Fu, “Pixel2mesh++: Multi-view 3dmesh generation via deformation,” in ICCV, 2019, pp. 1042–1051.
[16] B. Jiang, J. Zhang, Y. Hong, J. Luo, L. Liu, and H. Bao, “Bcnet:Learning body and cloth shape from a single image,” in ECCV,2020, pp. 18–35.
[17] N. Wang, Y. Zhang, Z. Li, Y. Fu, H. Yu, W. Liu, X. Xue, and Y.-G.Jiang, “Pixel2mesh: 3d mesh model generation via image guideddeformation,” IEEE TPAMI, vol. 43, no. 10, pp. 3600–3613, 2020.
[18] F. Tong, M. Nakao, S. Wu, M. Nakamura, and T. Matsuda, “Xray2shape: reconstruction of 3d liver shape from a single 2dprojection image,” in 2020 42nd EMBC, 2020, pp. 1608–1611.
[19] X. Li, K. Ping, X. Gu, and M. He, “3d shape reconstruction offurniture object from a single real indoor image,” in 2020 17thICCWAMTIP, 2020, pp. 101–104.
[20] Y. Dongsheng, K. Ping, and X. Gu, “3D Reconstruction based onGAT from a Single Image,” in ICCWAMTIP, 2020, pp. 122–125.
[21] Z. Zhang, Y. Wang, P. K. Jimack, and H. Wang, “MeshingNet:A New Mesh Generation Method Based on Deep Learning,” inICCS, 2020, pp. 186–198.
[22] Z. Wang, V. Isler, and D. D. Lee, “Surface Hof: Surface Reconstruction From A Single Image Using Higher Order FunctionNetworks,” in ICIP, 2020, pp. 2666–2670.
[23] P. Henderson, V. Tsiminaki, and C. H. Lampert, “Leveraging 2DData to Learn Textured 3D Mesh Generation,” in CVPR, Jun.2020, pp. 7495–7504.
[24] G. Yang, D. Sun, V. Jampani, D. Vlasic, F. Cole, H. Chang, D. Ramanan, W. T. Freeman, and C. Liu, “Lasr: Learning articulatedshape reconstruction from a monocular video,” in CVPR, 2021,pp. 15 980–15 989.
[25] U. Wickramasinghe, P. Fua, and G. Knott, “Deep active surfacemodels,” in CVPR, 2021, pp. 11 652–11 661.
[26] D. Smirnov, M. Bessmeltsev, and J. Solomon, “Learning manifoldpatch-based representations of man-made shapes,” in ICLR, 2020.
[27] H. Bertiche, M. Madadi, and S. Escalera, “Deep Parametric Surfaces for 3D Outfit Reconstruction from Single View Image,” inFG 2021, 2021, pp. 1–8.
[28] R. Li, S. Karanam, R. Li, T. Chen, B. Bhanu, and Z. Wu, “LearningLocal Recurrent Models for Human Mesh Recovery,” in 3DV,2021, pp. 555–564.
[29] M. Pedone, A. Mostafa, and J. Heikkila, “Learning non-rigid ¨surface reconstruction from spatia-temporal image patches,” inICPR, 2021, pp. 10 134–10 140.
[30] M. Hu, J. Rutqvist, and C. I. Steefel, “Mesh generation andoptimization from digital rock fractures based on neural styletransfer,” J. Rock Mech. Geotech. Eng., vol. 13, Aug. 2021.
[31] N. Wang, Y. Zhang, Z. Li, Y. Fu, H. Yu, W. Liu, X. Xue, and Y.-G. Jiang, “Pixel2Mesh: 3D Mesh Model Generation via ImageGuided Deformation,” IEEE TPAMI, vol. 43, pp. 3600–3613, 2021.
[32] J. Tang, X. Han, M. Tan, X. Tong, and K. Jia, “Skeletonnet: Atopology-preserving solution for learning mesh reconstruction ofobject surfaces from rgb images,” IEEE TPAMI, 2021.
[33] B. Jiang, Y. Hong, H. Bao, and J. Zhang, “Selfrecon: Self reconstruction your digital avatar from monocular video,” in CVPR,2022, pp. 5605–5615.
[34] T. Ben Charrada, H. Tabia, A. Chetouani, and H. Laga, “TopoNet:Topology Learning for 3D Reconstruction of Objects of ArbitraryGenus,” Comput Graph Forum, no. n/a, Mar. 2022.
[35] W. Wang, D. Ceylan, R. Mech, and U. Neumann, “3dn: 3ddeformation network,” in CVPR, 2019, pp. 1038–1046.
[36] T. Rios, J. Kong, B. van Stein, T. Back, P. Wollstadt, B. Sendhoff, ¨and S. Menzel, “Back To Meshes: Optimal Simulation-ready MeshPrototypes For Autoencoder-based 3D Car Point Clouds,” inSSCI, 2020, pp. 942–949.
[37] R. Hanocka, G. Metzer, R. Giryes, and D. Cohen-Or,“Point2Mesh: A Self-Prior for Deformable Meshes,” ACM TOG,vol. 39, no. 4, Aug. 2020.
[38] K. Gupta and M. Chandraker, “Neural mesh flow: 3D manifoldmesh generation via diffeomorphic flows,” in NeurIPS, Dec. 2020,pp. 1747–1758.
[39] B. Ma, Z. Han, Y.-S. Liu, and M. Zwicker, “Neural-Pull: LearningSigned Distance Functions from Point Clouds by Learning to PullSpace onto Surfaces,” ICML, vol. 139, Jan. 2021.
[40] U. Wickramasinghe, E. Remelli, G. Knott, and P. Fua,“Voxel2mesh: 3d mesh model generation from volumetric data,”in MICCAI, 2020, pp. 299–308.
[41] D. Du, X. Han, H. Fu, F. Wu, Y. Yu, S. Cui, and L. Liu, “SAniHead: Sketching Animal-Like 3D Character Heads Using a ViewSurface Collaborative Mesh Generative Network,” IEEE TVCG,vol. 28, no. 6, pp. 2415–2429, Jun. 2022.
[42] A. Chang-Hoi, L. Sang-Soo, L. Hyuek-Jae, and L. Soo-Young,“A self-organizing neural network approach for automatic meshgeneration,” IEEE Trans. Magn., vol. 27, pp. 4201–4204, Sep. 1991.
[43] D. Lowther and D. Dyck, “A density driven mesh generatorguided by a neural network,” IEEE Trans. Magn., vol. 29, no. 2,pp. 1927–1930, Mar. 1993.
[44] S. Alfonzetti, S. Coco, S. Cavalieri, and M. Malgeri, “Automaticmesh generation by the let-it-grow neural network,” IEEE Trans.Magn., vol. 32, no. 3, pp. 1349–1352, 1996.
[45] S. Alfonzetti, “A finite element mesh generator based on anadaptive neural network,” IEEE Trans. Magn., vol. 34, no. 5, pp.3363–3366, Sep. 1998.
[46] ——, “A neural network generator for tetrahedral meshes,” IEEETrans. Magn., vol. 39, no. 3, pp. 1650–1653, 2003.
[47] L. W. Peng and S. M. Shamsuddin, “3D object reconstruction andrepresentation using neural networks,” in GRAPHITE, 2004, pp.139–147.
[48] S. Yao, B. Yan, B. Chen, and Y. Zeng, “An ann-based elementextraction method for automatic mesh generation,” Expert Syst.Appl., vol. 29, no. 1, pp. 193–206, 2005.
[49] S. Alfonzetti, E. Dilettoso, and N. Salerno, “An Optimized Generator of Finite Element Meshes Based on a Neural Network,”IEEE Trans. Magn., vol. 44, pp. 1278–1281, Jun. 2008.
[50] G.-x. Li, X.-m. Wu, and W.-m. Zhao, “Incomplete Points CloudData Surface Reconstruction Based on Neural Network,” in IIHMSP, 2008, pp. 913–916.
[51] A. de Medeiros Brito Junior, A. D. DOria Neto, J. Dantas de Melo, ´and L. M. Garcia Goncalves, “An Adaptive Learning Approachfor 3-D Surface Reconstruction From Point Clouds,” IEEE Trans.Neural Netw., vol. 19, pp. 1130–1140, 2008.
[52] P. Wen, X. Wu, Y. Zhu, and X. Peng, “LS-RBF network based 3Dsurface reconstruction method,” in CCDC, Jun. 2009, pp. 5785–5789, iSSN: 1948-9447.
[53] S. Xiong, J. Zhang, J. Zheng, J. Cai, and L. Liu, “Robust surfacereconstruction via dictionary learning,” ACM TOG, vol. 33, no. 6,pp. 201:1–201:12, Nov. 2014.
[54] Z. Lun, M. Gadelha, E. Kalogerakis, S. Maji, and R. Wang, “3dshape reconstruction from sketches via multi-view convolutionalnetworks,” in 3DV, 2017, pp. 67–77.
[55] A. Sinha, A. Unmesh, Q. Huang, and K. Ramani, “Surfnet:Generating 3d shape surfaces using deep residual networks,” inCVPR, 2017, pp. 6040–6049.
[56] T. Groueix, M. Fisher, V. G. Kim, B. C. Russell, and M. Aubry,“A papier-mach ˆ e approach to learning 3d surface generation,” in ´CVPR, 2018, pp. 216–224.19
[57] C. Li, H. Pan, Y. Liu, X. Tong, A. Sheffer, and W. Wang, “Robustflow-guided neural prediction for sketch-based freeform surfacemodeling,” ACM TOG, vol. 37, no. 6, pp. 1–12, 2018.
[58] Y. Liao, S. Donne, and A. Geiger, “Deep Marching Cubes: Learn- ´ing Explicit Surface Representations,” in CVPR, Jun. 2018, pp.2916–2925.
[59] A. Ranjan, T. Bolkart, S. Sanyal, and M. J. Black, “Generating 3dfaces using convolutional mesh autoencoders,” in ECCV, 2018,pp. 704–720.
[60] Y.-P. Cao, Z.-N. Liu, Z.-F. Kuang, L. Kobbelt, and S.-M. Hu,“Learning to reconstruct high-quality 3d shapes with cascadedfully convolutional networks,” in ECCV, 2018, pp. 616–633.
[61] L. Mescheder, M. Oechsle, M. Niemeyer, S. Nowozin, andA. Geiger, “Occupancy networks: Learning 3d reconstruction infunction space,” in CVPR, 2019, pp. 4460–4470.
[62] G. Bouritsas, S. Bokhnyak, S. Ploumpis, M. Bronstein, andS. Zafeiriou, “Neural 3d morphable models: Spiral convolutionalnetworks for 3d shape representation learning and generation,”in ICCV, 2019, pp. 7213–7222.
[63] T. Li, Y. Shi, X. Sun, J. Wang, and B. Yin, “PGAN: PredictionGenerative Adversarial Nets for Meshes,” in VCIP, 2019, pp. 1–4.
[64] Q. Xu, W. Wang, D. Ceylan, R. Mech, and U. Neumann, “DISN:Deep Implicit Surface Network for High-quality Single-view 3DReconstruction,” in NeurIPS, vol. 32, 2019.
[65] Z. Chen and H. Zhang, “Learning Implicit Fields for GenerativeShape Modeling,” in CVPR, Jun. 2019, pp. 5932–5941.
[66] A. Dai and M. Nießner, “Scan2Mesh: From Unstructured RangeScans to 3D Meshes,” in CVPR, Jun. 2019, pp. 5569–5578.
[67] F. Williams, T. Schneider, C. Silva, D. Zorin, J. Bruna, andD. Panozzo, “Deep Geometric Prior for Surface Reconstruction,”in CVPR, Jun. 2019, pp. 10 122–10 131.
[68] J. J. Park, P. Florence, J. Straub, R. Newcombe, and S. Lovegrove,“Deepsdf: Learning continuous signed distance functions forshape representation,” in CVPR, 2019, pp. 165–174.
[69] R. Wu, Y. Zhuang, K. Xu, H. Zhang, and B. Chen, “Pq-net: Agenerative part seq2seq network for 3d shapes,” in CVPR, 2020,pp. 829–838.
[70] C. Nash, Y. Ganin, S. M. A. Eslami, and P. Battaglia, “PolyGen:An autoregressive generative model of 3D meshes,” in ICML, vol.1. PMLR, 2020, pp. 7220–7229.
[71] A. Hertz, R. Hanocka, R. Giryes, and D. Cohen-Or, “Deep geometric texture synthesis,” ACM TOG, vol. 39, pp. 108–1, 2020.
[72] H.-T. D. Liu, V. G. Kim, S. Chaudhuri, N. Aigerman, and A. Jacobson, “Neural subdivision,” ACM TOG, vol. 39, pp. 124–1, 2020.
[73] X. Yang, L. Zhou, H. Jiang, Z. Tang, Y. Wang, H. Bao, andG. Zhang, “Mobile3drecon: real-time monocular 3d reconstruction on a mobile phone,” IEEE TVCG, vol. 26, no. 12, pp. 3446–3456, 2020.
[74] M. Atzmon and Y. Lipman, “Sal: Sign agnostic learning of shapesfrom raw data,” in CVPR, 2020, pp. 2565–2574.
[75] A. Badki, O. Gallo, J. Kautz, and P. Sen, “Meshlet priors for 3dmesh reconstruction,” in CVPR, 2020, pp. 2849–2858.
[76] C. Jiang, A. Sud, A. Makadia, J. Huang, M. Nießner,T. Funkhouser et al., “Local implicit grid representations for 3dscenes,” in CVPR, 2020, pp. 6001–6010.
[77] S. Peng, M. Niemeyer, L. Mescheder, M. Pollefeys, and A. Geiger,“Convolutional occupancy networks,” in ECCV, 2020, pp. 523–540.
[78] G. Yan, Z. Chen, J. Yang, and H. Wang, “Interactive liquid splashmodeling by user sketches,” TOG, vol. 39, pp. 1–13, 2020.
[79] M. Liu, X. Zhang, and H. Su, “Meshing Point Clouds withPredicted Intrinsic-Extrinsic Ratio Guidance,” in ECCV. SpringerInternational Publishing, 2020, pp. 68–84.
[80] P. Erler, P. Guerrero, S. Ohrhallinger, N. J. Mitra, and M. Wimmer,“Points2Surf Learning Implicit Surfaces from Point Clouds,” inECCV, 2020, pp. 108–124.
[81] J. Gao, W. Chen, T. Xiang, A. Jacobson, M. McGuire, and S. Fidler,“Learning Deformable Tetrahedral Meshes for 3D Reconstruction,” in NeurIPS, vol. 33, 2020, pp. 9936–9947.
[82] N. Sharp and M. Ovsjanikov, “PointTriNet: Learned Triangulation of 3D Point Sets,” in ECCV, 2020, pp. 762–778.
[83] R. Daroya, R. Atienza, and R. Cajote, “REIN: Flexible MeshGeneration from Point Clouds,” in CVPRW, Jun. 2020, pp. 1444–1453.
[84] Z. Mi, Y. Luo, and W. Tao, “SSRNet: Scalable 3D Surface Reconstruction Network,” in CVPR, Jun. 2020, pp. 967–976.
[85] Y.-J. Yuan, Y.-K. Lai, J. Yang, Q. Duan, H. Fu, and L. Gao, “MeshVariational Autoencoders with Edge Contraction Pooling,” inCVPRW, Jun. 2020, pp. 1105–1112.
[86] J. Chibane, G. Pons-Moll et al., “Neural unsigned distance fieldsfor implicit function learning,” NeurIPS, vol. 33, pp. 21 638–21 652, 2020.
[87] E. Remelli, A. Lukoianov, S. Richter, B. Guillard, T. Bagautdinov,P. Baque, and P. Fua, “Meshsdf: Differentiable iso-surface extraction,” NeurIPS, vol. 33, pp. 22 468–22 478, 2020.
[88] A. Bozic, P. Palafox, J. Thies, A. Dai, and M. Nießner, “Transformerfusion: Monocular rgb scene reconstruction using transformers,” NeurIPS, vol. 34, pp. 1403–1414, 2021.
[89] R. Venkatesh, T. Karmali, S. Sharma, A. Ghosh, R. V. Babu,L. A. Jeni, and M. Singh, “Deep implicit surface point predictionnetworks,” in ICCV, 2021, pp. 12 653–12 662.
[90] J. Sun, Y. Xie, L. Chen, X. Zhou, and H. Bao, “Neuralrecon:Real-time coherent 3d reconstruction from monocular video,” inCVPR, 2021, pp. 15 598–15 607.
[91] J. Tang, J. Lei, D. Xu, F. Ma, K. Jia, and L. Zhang, “Saconvonet: Sign-agnostic optimization of convolutional occupancynetworks,” in ICCV, 2021, pp. 6504–6513.
[92] T. Shen, J. Gao, K. Yin, M.-Y. Liu, and S. Fidler, “Deep marchingtetrahedra: a hybrid representation for high-resolution 3d shapesynthesis,” in NeurIPS, vol. 34, 2021, pp. 6087–6101.
[93] S. Song, Z. Cui, and R. Qin, “Vis2mesh: Efficient mesh reconstruction from unstructured point clouds of large scenes with learnedvirtual view visibility,” in ICCV, 2021, pp. 6514–6524.
[94] S.-L. Liu, H.-X. Guo, H. Pan, P.-S. Wang, X. Tong, and Y. Liu,“Deep implicit moving least-squares functions for 3d reconstruction,” in CVPR, 2021, pp. 1788–1797.
[95] Y. Siddiqui, J. Thies, F. Ma, Q. Shan, M. Nießner, and A. Dai,“Retrievalfuse: Neural 3d scene reconstruction with a database,”in ICCV, 2021, pp. 12 568–12 577.
[96] Y. Luo, Z. Mi, and W. Tao, “Deepdt: Learning geometry from delaunay triangulation for surface reconstruction,” in AAAI, vol. 35,no. 3, 2021, pp. 2277–2285.
[97] W. Yifan, S. Wu, C. Oztireli, and O. Sorkine-Hornung, “Isopoints: Optimizing neural implicit surfaces with hybrid representations,” in CVPR, 2021, pp. 374–383.
[98] M.-J. Rakotosaona, N. Aigerman, N. J. Mitra, M. Ovsjanikov, andP. Guerrero, “Differentiable surface triangulation,” ACM TOG,vol. 40, no. 6, pp. 1–13, 2021.
[99] S. Peng, C. Jiang, Y. Liao, M. Niemeyer, M. Pollefeys, andA. Geiger, “Shape as points: A differentiable poisson solver,”NeurIPS, vol. 34, pp. 13 032–13 044, 2021.
[100] A. Boulch, P.-A. Langlois, G. Puy, and R. Marlet, “NeeDrop:Self-supervised Shape Representation from Sparse Point Cloudsusing Needle Dropping,” in 3DV, 2021, pp. 940–950.
[101] J. Lei, K. Jia, and Y. Ma, “Learning and Meshing from DeepImplicit Surface Networks Using an Efficient Implementation ofAnalytic Marching,” IEEE TPAMI, pp. 1–1, 2021.
[102] X. Wei, Z. Chen, Y. Fu, Z. Cui, and Y. Zhang, “Deep Hybrid SelfPrior for Full 3D Mesh Generation,” ICCV, 2021.
[103] J. Huang, S.-S. Huang, H. Song, and S.-M. Hu, “DI-Fusion: OnlineImplicit 3D Reconstruction with Deep Priors,” in CVPR, Jun.2021, pp. 8928–8937.
[104] M.-J. Rakotosaona, P. Guerrero, N. Aigerman, N. Mitra, andM. Ovsjanikov, “Learning Delaunay Surface Elements for MeshReconstruction,” in CVPR, Jun. 2021, pp. 22–31.
[105] A. Dielen, I. Lim, M. Lyon, and L. Kobbelt, “Learning DirectionFields for Quad Mesh Generation,” Comput Graph Forum, vol. 40,no. 5, pp. 181–191, Aug. 2021.
[106] R. Sulzer, L. Landrieu, R. Marlet, and B. Vallet, “Scalable SurfaceReconstruction with Delaunay-Graph Neural Networks,” ComputGraph Forum, vol. 40, no. 5, pp. 157–167, Aug. 2021.
[107] Z. Chen and H. Zhang, “Neural Marching Cubes,” ACM TOG,vol. 40, no. 6, pp. 1–15, Dec. 2021.
[108] J. Munkberg, J. Hasselgren, T. Shen, J. Gao, W. Chen, A. Evans,T. Muller, and S. Fidler, “Extracting triangular 3d models, mate- ¨rials, and lighting from images,” in CVPR, 2022, pp. 8280–8290.
[109] P. Mittal, Y.-C. Cheng, M. Singh, and S. Tulsiani, “Autosdf: Shapepriors for 3d completion, reconstruction and generation,” inCVPR, 2022, pp. 306–315.
[110] F. Williams, Z. Gojcic, S. Khamis, D. Zorin, J. Bruna, S. Fidler, andO. Litany, “Neural fields as learnable kernels for 3d reconstruction,” in CVPR, 2022, pp. 18 500–18 510.
[111] Z. Deng, Y. Liu, H. Pan, W. Jabi, J. Zhang, and B. Deng,“Sketch2PQ: Freeform Planar Quadrilateral Mesh Design via aSingle Sketch,” IEEE TVCG, pp. 1–1, 2022.
[112] S. Hahner and J. Garcke, “Mesh Convolutional Autoencoder forSemi-Regular Meshes of Different Sizes,” in WACV, 2022, pp.2344–2353.
[113] B. Ma, Y.-S. Liu, and Z. Han, “Reconstructing surfaces for sparsepoint clouds with on-surface priors,” in CVPR, 2022, pp. 6315–6325.
[114] P. Lu, N. Wang, Y. Lin, X. Zhang, Y. Wu, and H. Zhang, “Anew unstructured hybrid mesh generation method based on BPANN,” J. Phys. Conf. Ser, 2022.
[115] X. Chen, T. Li, Q. Wan, X. He, C. Gong, Y. Pang, and J. Liu,“MGNet: a novel differential mesh generation method based onunsupervised neural networks,” Eng. Comput., Mar. 2022.
[116] J. Pan, J. Huang, G. Cheng, and Y. Zeng, “Reinforcement learningfor automatic quadrilateral mesh generation: a soft actor-criticapproach,” Mar. 2022.
[117] Z. Chen, A. Tagliasacchi, T. Funkhouser, and H. Zhang, “NeuralDual Contouring,” ACM TOG, vol. 41, pp. 1–13, Jul. 2022.
[118] T. Li, Y. Shi, X. Sun, J. Wang, and B. Yin, “PCGAN: PredictionCompensation Generative Adversarial Network for Meshes,”IEEE T-CSVT, vol. 32, no. 7, pp. 4667–4679, Jul. 2022.
[119] Z. Zhu, S. Peng, V. Larsson, W. Xu, H. Bao, Z. Cui, M. R. Oswald,and M. Pollefeys, “Nice-slam: Neural implicit scalable encodingfor slam,” in CVPR, 2022, pp. 12 786–12 796.
[120] D. Azinovic, R. Martin-Brualla, D. B. Goldman, M. Nießner, and ´J. Thies, “Neural rgb-d surface reconstruction,” in CVPR, 2022,pp. 6290–6301.
[121] A. Boulch and R. Marlet, “Poco: Point convolution for surfacereconstruction,” in CVPR, 2022, pp. 6302–6314.
[122] W. E. Lorensen and H. E. Cline, “Marching cubes: A high resolution 3d surface construction algorithm,” ACM siggraph computergraphics, vol. 21, no. 4, pp. 163–169, 1987.
[123] A. Doi and A. Koide, “An efficient method of triangulating equivalued surfaces by using tetrahedral cells,” IEICE Trans. Inf. Syst.,vol. 74, pp. 214–224, 1991.
[124] M. Kazhdan and H. Hoppe, “Screened poisson surface reconstruction,” ACM TOG, vol. 32, no. 3, pp. 1–13, 2013.
[125] P. Wang, L. Liu, Y. Liu, C. Theobalt, T. Komura, and W. Wang,“Neus: Learning neural implicit surfaces by volume renderingfor multi-view reconstruction,” in NeurIPS.
[126] J. Wang, T. Bleja, and L. Agapito, “Go-surf: Neural feature gridoptimization for fast, high-fidelity rgb-d surface reconstruction,”in 3DV, 2022, pp. 433–442.
[127] S. J. Ruuth and B. Merriman, “A simple embedding method forsolving partial differential equations on surfaces,” J Comput Phys,vol. 227, no. 3, pp. 1943–1961, 2008.
[128] C. B. Macdonald and S. J. Ruuth, “Level set equations on surfacesvia the closest point method,” J. Sci. Comput., vol. 35, pp. 219–240,2008.
[129] ——, “The implicit closest point method for the numerical solution of partial differential equations on surfaces,” SIAM Journalon Scientific Computing, vol. 31, no. 6, pp. 4330–4350, 2010.
[130] T. Marz and C. B. Macdonald, “Calculus on surfaces with general ¨closest point functions,” SINUM, vol. 50, pp. 3303–3328, 2012.
[131] L. Tian, C. B. Macdonald, and S. J. Ruuth, “Segmentation onsurfaces with the closest point method,” in ICIP, 2009, pp. 3009–3012.
[132] C. B. Macdonald, J. Brandman, and S. J. Ruuth, “Solving eigenvalue problems on curved surfaces using the closest pointmethod,” J Comput Phys, vol. 230, no. 22, pp. 7944–7956, 2011.
[133] D.-T. Lee and B. J. Schachter, “Two algorithms for constructinga delaunay triangulation,” In. j. comput. inf. sci., vol. 9, no. 3, pp.219–242, 1980.
[134] N. Ray, W. C. Li, B. Levy, A. Sheffer, and P. Alliez, “Periodic global ´parameterization,” ACM TOG, vol. 25, no. 4, pp. 1460–1485, 2006.
[135] X. Gu, S. J. Gortler, and H. Hoppe, “Geometry images,” inProceedings of the 29th annual conference on Computer graphics andinteractive techniques, 2002, pp. 355–361.
[136] I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. WardeFarley, S. Ozair, A. Courville, and Y. Bengio, “Generative adversarial networks,” Commun. ACM, vol. 63, pp. 139–144, 2020.
[137] R. Lohner and P. Parikh, “Generation of three-dimensional un- ¨structured grids by the advancing-front method,” Int. J. Numer.Methods Fluids, vol. 8, no. 10, pp. 1135–1149, 1988.
[138] Y. Guo, X. Huang, Z. Ma, Y. Hai, R. Zhao, and K. Sun, “Animproved advancing-front-delaunay method for triangular meshgeneration,” in CGI, 2021, pp. 477–487.
[139] T. Ju, F. Losasso, S. Schaefer, and J. Warren, “Dual contouring ofhermite data,” in SIGGRAPH, 2002, pp. 339–346.
[140] D. P. Kingma and M. Welling, “Auto-encoding variational bayes,”arXiv preprint arXiv:1312.6114, 2013.
[141] H. Fan, H. Su, and L. J. Guibas, “A point set generation networkfor 3d object reconstruction from a single image,” in CVPR, 2017,pp. 605–613.
[142] O. Sorkine, D. Cohen-Or, and S. Toledo, “High-pass quantizationfor mesh encoding.” in SGP, vol. 42, 2003, p. 3.
[143] I. Abouelaziz, M. El Hassouni, and H. Cherifi, “A curvaturebased method for blind mesh visual quality assessment usinga general regression neural network,” in SITIS. IEEE, 2016, pp.793–797.
[144] I. Abouelaziz, M. E. Hassouni, and H. Cherifi, “A convolutionalneural network framework for blind mesh visual quality assessment,” in ICIP, Sep. 2017, pp. 755–759.
[145] I. Abouelaziz, A. Chetouani, M. El Hassouni, and H. Cherifi,“Reduced Reference Mesh Visual Quality Assessment Based onConvolutional Neural Network,” in SITIS, 2018, pp. 617–620.
[146] I. Abouelaziz, A. Chetouani, M. E. Hassouni, L. J. Latecki, andH. Cherifi, “Convolutional Neural Network for Blind Mesh Visual Quality Assessment Using 3D Visual Saliency,” in ICIP, 2018.
[147] I. Abouelaziz, A. Chetouani, M. El Hassouni, H. Cherifi, andL. J. Latecki, “Learning graph convolutional network for blindmesh visual quality assessment,” IEEE Access, vol. 9, pp. 108 200–108 211, 2021.
[148] X. Chen, J. Liu, Y. Pang, J. Chen, L. Chi, and C. Gong, “Developing a new mesh quality evaluation method based on convolutional neural network,” Eng. Appl. Comput. Fluid Mech, vol. 14,no. 1, pp. 391–400, 2020.
[149] X. Chen, J. Liu, C. Gong, S. Li, Y. Pang, and B. Chen, “Mve-net:An automatic 3-d structured mesh validity evaluation frameworkusing deep neural networks,” Comput Aided Des, vol. 141, p.103104, 2021.
[150] A. X. Chang, T. Funkhouser, L. Guibas, P. Hanrahan, Q. Huang,Z. Li, S. Savarese, M. Savva, S. Song, H. Su et al., “Shapenet: Aninformation-rich 3d model repository,” arXiv preprint, 2015.
[151] A. M. Bronstein, M. M. Bronstein, and R. Kimmel, “Efficientcomputation of isometry-invariant distances between surfaces,”SIAM J. Sci. Comput, vol. 28, pp. 1812–1836, 2006.
[152] Y. Wang, S. Asafi, O. Van Kaick, H. Zhang, D. Cohen-Or, andB. Chen, “Active co-analysis of a set of shapes,” ACM TOG,vol. 31, no. 6, pp. 1–10, 2012.
[153] M. Berger, J. A. Levine, L. G. Nonato, G. Taubin, and C. T. Silva,“A benchmark for surface reconstruction,” ACM TOG, vol. 32,no. 2, pp. 1–17, 2013.
[154] Q. Zhou and A. Jacobson, “Thingi10k: A dataset of 10,000 3dprinting models,” arXiv preprint arXiv:1605.04797, 2016.
[155] F. Bogo, J. Romero, G. Pons-Moll, and M. J. Black, “Dynamicfaust: Registering human bodies in motion,” in CVPR, 2017, pp.6233–6242.
[156] S. Koch, A. Matveev, Z. Jiang, F. Williams, A. Artemov, E. Burnaev, M. Alexa, D. Zorin, and D. Panozzo, “Abc: A big cad modeldataset for geometric deep learning,” in CVPR, 2019, pp. 9601–9611.
[157] X. Sun, J. Wu, X. Zhang, Z. Zhang, C. Zhang, T. Xue, J. B.Tenenbaum, and W. T. Freeman, “Pix3d: Dataset and methodsfor single-image 3d shape modeling,” in CVPR, 2018, pp. 2974–2983.
[158] J. Booth, A. Roussos, S. Zafeiriou, A. Ponniah, and D. Dunaway,“A 3d morphable model learnt from 10,000 faces,” in CVPR, 2016,pp. 5543–5552.
[159] Y. Zheng, R. Shao, Y. Zhang, T. Yu, Z. Zheng, Q. Dai, and Y. Liu,“Deepmulticap: Performance capture of multiple characters using sparse multiview cameras,” in ICCV, 2021, pp. 6239–6249.
[160] “Renderpeople,” <https://renderpeople.com/free-3d-people>.
[161] “axyz,” <https://secure.axyz-design.com/>, 2019.
[162] A. Dai, A. X. Chang, M. Savva, M. Halber, T. Funkhouser, andM. Nießner, “Scannet: Richly-annotated 3d reconstructions ofindoor scenes,” in CVPR, 2017, pp. 5828–5839.
[163] A. Handa, V. Patr ˘ aucean, S. Stent, and R. Cipolla, “Scenenet: An ˘annotated model generator for indoor scene understanding,” inICRA, 2016, pp. 5737–5743.
[164] A. Chang, A. Dai, T. Funkhouser, M. Halber, M. Niessner,M. Savva, S. Song, A. Zeng, and Y. Zhang, “Matterport3d: Learning from rgb-d data in indoor environments,” arXiv preprint, 2017.
[165] N. Pietroni, S. Nuvoli, T. Alderighi, P. Cignoni, and M. Tarini,“Reliable feature-line driven quad-remeshing,” in ACM SIGGRAPH, vol. 40, no. 4, 2021, pp. 1–17.
[166] D. Maturana and S. Scherer, “Voxnet: A 3d convolutional neuralnetwork for real-time object recognition,” in IROS, 2015, pp. 922–928.
[167] A. Brock, T. Lim, J. M. Ritchie, and N. Weston, “Generativeand discriminative voxel modeling with convolutional neuralnetworks,” arXiv preprint arXiv:1608.04236, 2016.
[168] P.-S. Wang, Y. Liu, Y.-X. Guo, C.-Y. Sun, and X. Tong, “Ocnn: Octree-based convolutional neural networks for 3d shapeanalysis,” ACM TOG, vol. 36, pp. 1–11, 2017.
[169] Z. Chen, V. G. Kim, M. Fisher, N. Aigerman, H. Zhang, andS. Chaudhuri, “Decor-gan: 3d shape detailization by conditionalrefinement,” in CVPR. ICS, 2021, pp. 15 735–15 744.
[170] C. R. Qi, H. Su, K. Mo, and L. J. Guibas, “Pointnet: Deep learningon point sets for 3d classification and segmentation,” in CVPR,2017, pp. 652–660.
[171] C. R. Qi, L. Yi, H. Su, and L. J. Guibas, “Pointnet++: Deephierarchical feature learning on point sets in a metric space,”NeurIPS, vol. 30, 2017.
[172] Y. Yang, C. Feng, Y. Shen, and D. Tian, “Foldingnet: Point cloudauto-encoder via deep grid deformation,” in CVPR, 2018, pp.206–215.
[173] H. Thomas, C. R. Qi, J.-E. Deschaud, B. Marcotegui, F. Goulette,and L. J. Guibas, “Kpconv: Flexible and deformable convolutionfor point clouds,” in ICCV, 2019, pp. 6411–6420.
[174] Y. Wang, Y. Sun, Z. Liu, S. E. Sarma, M. M. Bronstein, and J. M.Solomon, “Dynamic graph cnn for learning on point clouds,”ACM Trans. Graph., vol. 38, no. 5, oct 2019.
[175] Z. Li, W. Wang, N. Lei, and R. Wang, “Weakly supervised pointcloud upsampling via optimal transport,” in ICASSP, 2022, pp.2564–2568.
[176] R. Wiersma, A. Nasikun, E. Eisemann, and K. Hildebrandt,“Deltaconv: anisotropic operators for geometric deep learning onpoint clouds,” ACM TOG, vol. 41, no. 4, pp. 1–10, 2022.
[177] R. Hanocka, A. Hertz, N. Fish, R. Giryes, S. Fleishman, andD. Cohen-Or, “Meshcnn: a network with an edge,” ACM TOG,vol. 38, no. 4, pp. 1–12, 2019.
[178] Y. Feng, Y. Feng, H. You, X. Zhao, and Y. Gao, “Meshnet: Meshneural network for 3d shape representation,” in AAAI, vol. 33,no. 01, 2019, pp. 8279–8286.
[179] F. Milano, A. Loquercio, A. Rosinol, D. Scaramuzza, andL. Carlone, “Primal-dual mesh convolutional neural networks,”NeurIPS, vol. 33, pp. 952–963, 2020.
[180] V. V. Singh, S. V. Sheshappanavar, and C. Kambhamettu, “Meshnet++: A network with a face,” in ACM MM, 2021, pp. 4883–4891.
[181] J. Masci, D. Boscaini, M. Bronstein, and P. Vandergheynst,“Geodesic convolutional neural networks on riemannian manifolds,” in ICCVW, 2015, pp. 37–45.
[182] D. Boscaini, J. Masci, E. Rodola, and M. Bronstein, “Learning `shape correspondence with anisotropic convolutional neural networks,” NeurIPS, 2016.
[183] I. Lim, A. Dielen, M. Campen, and L. Kobbelt, “A simple approach to intrinsic correspondence learning on unstructured 3dmeshes,” in ECCVW, 2018, pp. 0–0.
[184] J. Schult, F. Engelmann, T. Kontogianni, and B. Leibe,“Dualconvmesh-net: Joint geodesic and euclidean convolutionson 3d meshes,” in CVPR, 2020, pp. 8612–8622.
[185] Y. Zhou, C. Wu, Z. Li, C. Cao, Y. Ye, J. Saragih, H. Li, andY. Sheikh, “Fully convolutional mesh autoencoder using efficientspatially varying kernels,” NeurIPS, vol. 33, pp. 9251–9262, 2020.
[186] D. Smirnov and J. Solomon, “Hodgenet: Learning spectral geometry on triangle meshes,” ACM TOG, vol. 40, pp. 1–11, 2021.
[187] N. Sharp, S. Attaiki, K. Crane, and M. Ovsjanikov, “Diffusionnet:Discretization agnostic learning on surfaces,” ACM TOG, vol. 41,no. 3, pp. 1–16, 2022.
[188] X. Zheng, Y. Zhu, W. Chen, N. Lei, Z. Luo, and X. Gu, “Quadrilateral mesh generation III: Optimizing singularity configurationbased on abel-jacobi theory,” Comput. Methods Appl. Mech. Eng.,vol. 387, p. 114146, 2021.
[189] N. Lei, K. Su, L. Cui, S.-T. Yau, and X. D. Gu, “A geometric viewof optimal transportation and generative model,” Comput. AidedGeom. Des, vol. 68, pp. 1–21, 2019.
[190] L. Gao, T. Wu, Y.-J. Yuan, M.-X. Lin, Y.-K. Lai, and H. Zhang,“Tm-net: Deep generative networks for textured meshes,” ACMTOG, vol. 40, no. 6, pp. 1–15, 2021.

链接:

引言

动机

相关调查

方法