自动摘要: 特征空间中的隐式函数应用在3D形状的重建和完成 [Chibane_ImplicitFunctionsinFeatureSpacefor3DShapeReconstruction ……..

特征空间中的隐式函数应用在3D形状的重建和完成

Chibane_Implicit Functions in Feature Space for 3D Shape Reconstruction and Completion.pdf

Chibane J, Alldieck T, Pons-Moll G. Implicit functions in feature space for 3d shape reconstruction and completion[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020: 6970-6981.

作者代码

翻译与修改的代码

摘要

虽然许多研究都专注于从图像中进行三维重建，但在本文中我们关注从各种三维输入中实现三维形状的重建和完成，因为这些三维输入在某些方面是存在缺陷的：低和高分辨率的体素、稀疏和稠密的点云，完整或者不完整的数据。而这类三维输入正是三维扫描仪的输出结果，而且获得这样的数据也越来越容易，并且它们还是三维计算机视觉算法的过渡数据，因此处理这种三维输入变得越来越重要。最近，学习隐式函数已经表现了巨大的可能，因为它们能够产生连续性的重建。然而，我们也从三维输入中发现了两个限制：

输入数据中存在的细节没有被保留；
多关节型的人体重建效果很差。

为了解决这个问题，我们提出了隐式特征网络（Implicit Feature Networks, IF-Nets），这种网络提供了连续的输出，能够处理多种拓扑结构，并且为稀疏的或者存在丢失的输入数据提供了完整的形状，保留了最近学习得到的隐式函数的良好特性，但是最为关键的是网络能够保留输入数据中存在的细节信息，并且能够重建多关节型人体。我们的工作与以往工作的两个关键区别：

抽取深度特征的一个可以学习的三维多尺度张量来代替单个矢量来编码三维形状，并且这个特征对齐了嵌入到形状中的原始的欧几里德空间；
从一个连续查询点的张量中抽取深度特征来代替点坐标来进行分类。这样的操作强迫我们的模型基于局部和全局形状结构而不是点坐标进行决策，点坐标在欧几里德变换下是随意的、缺少先验结构的。

实验表明，基于ShapeNet数据集，IF-Nets明显优于现有的三维物体重建方法，并且获得了更加精确的三维人体重建。代码参考：Implicit Feature Networks。

图1：使用我们的方法的结果。（左）：稀疏的体素重建；（中）：稠密的体素重建；（右）：三维单视角点云重建（后背遮挡）。我们的方法发现了连续的输出，处理了多重拓扑（右），并且保存了（中）与（右）的输入细节，在人体关节上效果很好，不像以前的工作。

Sec01 介绍

虽然许多工作专注在基于图像的三维重建[^23]，但是在本文中我们专注于从各种三维输入中实现三维表面重建和形状完成，这些输入在某些方面存在不足：低分辨率体素网格、高分辨率体素网格、稀疏的和稠密的点云、完整或者不完整的数据。随着三维扫描技术越来越普及，这样的输入也变得无所不在，它们通常是三维计算机视觉算法中的中间输出。然而，大多数应用程序的最终输出应该是可渲染的连续的和完整的曲面，这是我们工作的重点。

对于稀疏网格和（不完整）的点云，基于学习的方法相比经典方法是更好的选择[6],[42]，因为它们对全局对象形状进行推理，但是也受到它们的输出表示的限制。

基于网格的方法通常学着将初始化的凸模板变形[^72]，并且其不能表示不同的拓扑。
基于体素的表示[11]，[39]需要占用大量的内存空间，这严重限制了输出的分辨率，输出的结果是缺少细节的粗糙形状。
基于点云的表示[54],[55]相比基于体素的表示效率更高，但在实现表面渲染和可视化时相对较难。

最近，隐式函数[48],[43],[^10]已经被证明是一种有前途的形状表示学习工具。其关键思想是，给定一个编码为向量的粗糙形状，和查询点的的坐标，学习一个函数用于决定点在形状的内部还是外部。学习后的隐函数可以在任意分辨率的三维查询点上求值，并且采用经典的移动立方体算法（Marching Cubes Algorithm，MCA）提取网格或者曲面。这种输出表示能够支持以任意的分辨率进行形状恢复，并且输出结果是连续的，可以处理不同的拓扑结果。

虽然这些方法在重建对齐的刚性物体时效果很好，但是我们观察到它们存在两个限制：

它们不能表示复杂的对象，例如：多关节人体（经常会遇到手臂或者大腿缺失）
它们不能保留输入数据中存在的细节。

我们认为发生这种情况是因为

网络在点坐标上学习了过强的先验，破坏了关节的方差；
形状编码向量缺少三维结构，导致解码看起来更像形状原型的分类[^66]，而不是连续性的回归。

因此，所有现存的基于学习的方法，无论它们是基于体素、网格、点或者隐式函数都存在某些方面的不足。

表1：最近的三维重建方法基于它们的输出表示进行分类，建立了它们的优点与缺点的一览表。体素、点云和网格是非连续性的，受离散化影响的。网格还含有固定的拓扑结构，这个特性限制了可以表示的三维形状的空间。最近的学习隐式函数的方法减轻了这些限制，但是无法保存细节信息或者重建关节。本文提出的IF-Nets方法在三维输入重建中拥有了隐式函数需要的性质，但是还额外地能够保存稠密三维输入中存在的细节信息，以及能够重建多关节型人体。

输出三维表示	连续输出	多种拓扑	稀疏输入	稠密输入	多关节型
体素	×	√	√	×	√
点云	×	√	√	×	√
网格	×	×	√	×	√
隐式函数	√	√	√	×	×
我们的方法	√	√	√	√	√

在本文中，我们提出了 IF-Nets，这个方法与以前的工作相比做好了5个方面（如表1所示）：它们是连续的，可以处理多重拓扑，可以为稀疏输入补全数据，保留隐式函数模型[48][43][10]的好的性质，但是最关键的是它们能够保留输入数据（稠密输入）中存在的细节，并且能够重建多关节型人体。IF-Nets与最近工作[48][43][10]有两个显著区别：

提取深度特征的多尺度三维张量代替单个向量来编码三维形状，这个特征对齐了嵌入在形状中的原始的欧几里德空间；
对连续查询点提取的深度特征分类，代替直接对点坐标分类

因此，不像以往的工作，IF-Nets不记忆通常的坐标位置，因为这种坐标位置基于欧几里德变换的结果是随意的。代替的方法是基于多尺度特征，围绕着点，对局部的或者全局的对象形状结构进行编码，然后基于这种编码进行决策。

为了描述 IF-Nets 的优点，我们首先证明了 IF-Nets 相比以前的方法可以更好地重建简单的刚性三维对象。对于多关节型人体，我们基于1600个人体的数据集上训练 IF-Nets 和相关的方法，数据集中包括不同的姿势、形状和衣着。与以往的方法形成鲜明的对比，在缺失的四肢未提供数据的情况下，IF-Nets 可以全局地重建多关节型对象，而且恢复了细节性结构（如：衣料的褶皱）。定量和定性的实验验证了 IF-Nets 在关节生成上更加鲁棒，并且在缺失精细尺度的细节时，生成全局一致的形状。为了推动在三维处理、学习和重建工作上的进一步研究，我们在Implicit Feature Networks - IF-Net (mpg.de)开源了 IF-Nets。

Sec02 相关工作

用于三维形状重建的方法分类

按照使用的表示方式分类为：体素、网格、点云和隐函数；
依据对象分类：刚性对象和人体

对于最新的、更加详尽的回顾，我们建议读者参考[^23]。表1中给出了近期三维重建方法的优缺点的简要概述。

Sec0201 体素表示

刚性对象的体素表示

由于体素是图像网格中像素的自然的三维扩展，并且允许三维卷积，因此它们经常用于生成和重建[29][26][57][46]。然而，内存占用通常与分辨率成立方比，这限制了早期的工作[75][11][68]在小型的
的网格中预测形状。在受限的训练批次和缓慢的训练或者有损的二维投影[63]代价下更高的分辨率应用在[74][73][8]。多分辨率[24][65][71]重建减少了内存占用，允许了大小的网格。然而，这些方法实现起来很复杂，需要对输入进行多次传递，并且仍然局限于大小的网格，这导致了可见的量化伪影。为了平滑噪声，有可能将形状表示为截断符号的距离函数（Truncated Signed Distance Functions，TSDF）[12]用于学习[14][36][58][^64]。然而，分辨率仍然受到存储TSDF值的三维网格的限制。

生成形状模型通常利用神经网络将一维矢量映射到体素表示[18][74]。和我们一样，[^40]的作者观察到一维矢量的限制较大，无法生成具有局部结构和全局结构的形状，于是他们引入了具有跳跃连接的层次隐编码。而我们提出了一个简单得多的三维多尺度特征张量，它与嵌入形状的原始的欧几里德空间对齐。

人体的体素表示

从图像的角度，基于体素的表示[70][17][82]或者基于深度图的表示[16][62][38]，CNN人体重建相比基于网格或者基于模板的表示产生了更多的细节，因为预测与输入在像素上对齐。不幸的是，这是以身体部件缺失为代价的。因此，一些方法[70][62]拟合表面多人线性（Skinned Multi-Person Linear，SMPL）模型作为重建的后处理步骤。然而，如果原始重建不太完整，处理很容易失败。所有这些方法都处理图像的像素，而我们则直接处理三维数据。这些方法受到体素网络分辨率的限制，而我们的方法则不受影响。

Sec0202 网格表示

刚性对象的网格表示

许多基于网格的方法将形状预测看作模型的变形[72][65]，因此受限于单个拓扑。或者，直接推导出网格（顶点和面片）[20][13]–虽然这个研究方向很有前途，但是这个方法的计算量非常大，并且不能保证输出没有交集的封闭网格。直接的网格预测也可以使用经典的移动立方体算法（Marching Cubes Algorithm，MCA）[42]的可学习版本[40]，但是这个方法也受限于潜在的小规模的体素网格。[^19]提出了一种有前途的体素与网格的组合，但是结果仍然粗糙。

人体的网格表示

自从引入了（基于网格的）SMPL人体模型[41]，越来越多的论文利用它从点云、深度数据和图像中重建形状和姿态[28][32][33][47][69][79]。由于SMPL没有服装和细节的模型，最近的方法对来自SMPL或者来自模板的模型预测变形。不幸的是，基于CNN的网格预测往往过于平滑。可以通过预测曲面的UV帖面/几何图像上的法线和位移图获得更多的细节[4][37][53]。然而，所有这些方法或者对于每一个新的服装拓扑采用不同的模板[7][49]，或者无法产生高质量的重建[^53]。

Sec0203 点云表示

刚性对象的点云表示

处理点云是一个重要的问题，因为它们是许多传感器（激光雷达、三维扫描仪）和计算机视觉算法的输出。由于它是轻量级的，因为在计算机图形学中也被广泛用于表示和操控形状[50]。基于PointNet的架构[54][55]是首先提出直接使用点云用于分类和语义分割。其思想是将一个全连接网络应用于每个点，然后执行一个全局池化操作，以满足数据排列不变性。最近的架构应用核化点卷积[67]、基于树的图卷积[60]和规范化流[77]。点云也用作重建[15][25]和生成[77]的形状表示。与体素与网格不同，点云需要使用经典的方法[6][30][31][^8]进行非平凡的后处理以获得可以渲染的曲面。

人体的点云表示

很少有研究使用点云表示人体[5]，可能是因为无法渲染。最近的研究要么使用PointNet架构[27]，要么使用基于点基的架构[^52]，实现人体网格到点云的对齐。

Sec0204 隐函数表示

刚性对象的隐函数表示

最近，神经网络被用于学习一个表示形状的连续的隐函数[43][48][10][44][35]，通过这种方式得到的神经网络可以输入一个隐编码和一个查询点
去预测TSDF值[48]或者点的二进制占用[43][10]。最近的方法[76]将三维查询点特征与局部图像特征相结合，通过视点预测近似地将查询点投影到二维图像中，实现了最先进的三维重建结果。这种在隐函数学习中使用的查询连续点的技巧允许在连续空间中（可能在任何分辨率下）进行预测，突破了基于体素的方法的内存限制。我们受到这些研究的启发，同时还注意到它们不能从三维数据中重建人体关节；[76]不能将点云或者体素网格作为三维输入，还依赖于三维到二维的投影的逼近（存在细节损失问题）；[43][10]的重建经常会丢失肢体。我们假设[43][10][76]只是记住了点的坐标而不是关于形状的推理，并且向量化的隐一维向量表示[43][^10]没有与输入对齐，还缺乏三维的结构。我们通过查询深度特征来解决这个问题，这个深度特征是多尺度特征的三维网格的连续位置中提取的，并且多尺度特征与三维输入空间是对齐的。这个修改很容易实现，并且获得了更好的重建质量。

人体的隐函数表示

TSDF[12]已经被用于表示人体形状，这类人体形状是用于深度整合和追踪[45][61]的研究。这样的隐表示已经与SMPL[41]人体模型结合起来使用，从而显著地提升了追踪的稳健性和精确度[78]。通过输入图像，我们使用隐式网络[59]来预测带衣服的人体，相比先前的隐函数[10]研究，产生了更高品质的结果。基于三维查询点和二维图像特征的位置，通过逐点占用预测来实现重建，对于简单的姿势，可以产生非常棒的和精细的结果；但是对于复杂的姿势则面临困难。[59]没有像我们这样集成了多尺度三维形状表示，它是为图像重建设计的，而我们则专注于从稀疏的和稠密的点云和占位网格中实现三维重建。像以前的隐式网络一样，我们的方法以任意分辨率生成连续曲面。但重要的是，由于我们的三维多尺度形状表示与输入空间对齐，所以我们的重建保留了整体结构，同时还保留了精细尺度的细节，即使是复杂的姿势。

Sec03 方法

为了推动我们的隐式特征网络（IF-Nets）的设计，我们首先描述了最近学习得到的隐式函数的公式，在Sec0301中指出它们的优势与劣势。在Sec0302中解释了IF-Nets。在图2中描述了IF-Nets的关键概念。

图2：IF-Nets的概览：给定一个（不完整的或者低分辨率的）输入，我们计算一个多尺度特征的三维网格，编码输入形状的全局和局部性质。然后，我们在连续点的位置从网格中抽取了深度特征。仅基于抽取的这些特征，解码器判断点是在曲面的内部（类别是1）或者外部（类别是0）。就如最近的基于隐函数的工作，我们可以在任意分辨率下查询，并且重建一个连续曲面。不像以前的方法使用点坐标进行推理，我们的方法仅基于逐点的深度特征。这允许我们去重建关节型结构，并且保留输入的细节。

Sec0301 背景：从隐性曲面中学习

当最近的工作[48][43][10]从3D输入中学习隐式重建时，它们的推理和输出的形状表示（有符号的距离或者二进制占用），在概念上是相似的。这里，我们描述了[43]中的占用公式。请注意，这些方法的优势和限制都是相似的。他们都使用一个隐向量编码三维形状。然后，形状的一个连续表示通过一个神经函数获得：

函数的输入为一个查询点和隐式编码，隐式编码用于分类点在曲面的内部（类别为1）还是外部（类别为0）。于是，曲面隐含地表示为点的决策面，其中为阈值参数（在IF-Nets中）。

函数一旦学习得到，就可以用于连续点位置的查询，不像典型的体素网格存在的分辨率限制。为了构造一个网格，移动立方体算法（Marching Cubes Algorithm，MCA）[^42]可以被应用在预测占用网格（Occupancy Grid）。这个优雅的公式打破了以前表示上的障碍，允许复杂拓扑结构的细节重建，并且在许多任务上（如：从图像、占用网格、点云中实现刚性物体重建）被证明有效。然而，我们也观测到这类模型存在两个限制：

它们无法表示复杂的对象，如：关节式物体；
它们无法保存输入数据的细节。

我们使用IF-Nets解决这些问题。

Sec0302 隐式特征网络

我们发现前面的公式存在的两个潜在的问题：

直接输入点坐标使用网络的推理可以绕过形状的结构，直接记忆典型的对象原型的点占用。这将严重损害旋转和平移的重建方差，而这个方差是用于分割、识别和检测的二维卷积网络的成功基石。
在单个向量中编码完整的形状会丢失数据中存在的细节，并且丢失了与嵌入形状的原始三维空间的对齐性质。

在本文中，我们提出了一个新颖的编码和解码串联操作，能够解决基于点云或者占用网格完成三维重建任务时存在的上述两个限制。给定一个对象的三维输入数据，其中描述了输入的空间，表示一个三维点，我们希望预测在对象的里面还是外面。

形状编码

为了替换在单个向量中编码形状，我们构建了数据的丰富编码。这个要求输入位于离散的体素网格上，即：，其中表示输入的分辨率。为了处理点云，我们先对其简单地离散化，然后对输入下采样，接着是卷积用于增加感受野和通道，同时降低分辨率，就如在二维上的惯常操作[^34]。反复地在输入数据上应用这个过程次后，我们创建了多尺度深度特征网格（Multi-Scale Deep Feature Grid），其中降低的分辨率，每个阶段的通道维度变量。在早期阶段（从开始）特征网格捕捉高频（形状细节），在后期阶段（以终止）特征网格拥有大范围的感受野，从而捕捉数据的全局结构。这样使得模型能够在获得输入中存在的细节时，对缺失的或者稀疏的数据进行推理。我们将编码器表示为：

形状解码

为了替换直接对点坐标进行分类，我们在位置从特征网格中抽取了学习到的深度特征。很有可能是因为我们的编码具有与输入数据对齐的三维结构，由于特征网格是离散的，我们使用三线性插值去查询连续的三维点。为了将局部近邻信息编码到点的编码中，即使只有小感受野（如：）的早期网格中，我们在查询点自身的位置处提取特征，此外还在沿着笛卡尔轴距离为的邻近点提取特征：

其中，是到中心点的距离，是第个笛卡尔坐标轴的单位向量，详见[补充材料](Implicit Functions in Feature Space for 3D Shape Reconstruction and Completion-Supplementary Material.md)中的描述。

然后，点编码被送入基于全连接神经网络参数化的逐点解码器去预测点在形状的内部还是外部：

比较公式（1）与（4），网络使用基于局部的和全局的形状特征替换了点的坐标对点进行分类，因为点的坐标在旋转、平移和关节型变换时是随意的。此外，我们的多尺度编码在推理全局形状的时候保留细节是可能的。

Sec0303 训练模型

为了训练等式（2）中的多尺度编码器和等式（4）中的解码器，其中是参数化的神经网络权重，是三维输入和对应的三维基准对象曲面的数据对，其中，描述的是这样的训练样例的数目。符号描述了在点的多尺度编码的估计。

为了创建训练点样本，对于每个基准曲面，我们抽样了个点，其中。为了这个目的，基准曲面首先要保证水密性。其次，计算基准占用，形状内部的点估计为1，形状外部的点估计为0。接下来，通过基准曲面上的采样点和增加的随机替换点，如：，在曲面附近创建点采样。为了这个目的，我们使用了对角协方差矩阵，其中。通过在曲面附近很小的抽样，在曲面周围较大的抽样可以得到好的结果。为了训练，优化得到的网络权重，通过最小化小批量损失：

其在给定的小批量的训练曲面和子样本的点样本上求和。对于小批量损失的每次估计，子样本是再生成的。对于，我们使用标准交叉熵损失。通过最小化，我们基于端到端的方式，联合训练编码器和解码器。实验中超参数使用的具体值请参考补充材料。

Sec0304 推理模型

在测试阶段，目标是在给定一个离散的和不完整的三维输入，重建一个连续的和完整的表示。首先，我们使用学习到的编码器网络去重建多尺度特征网格。然后，我们使用逐点解码器网格在连续的点位置（参见Sec0302）去创建占用预测。为了重建网格，我们基于需要的分辨率的网格在点上估计了IF-Nets。然后，输出的高分辨率占用网格被变换到一个使用经典MCA算法[^42]的网格。

Sec04 实验

在本节中，我们验证了IF-Nets在三维形状重建任务中的有效性。事实证明，IF-Nets可以解决最近的基于学习的方法在这类任务上存在的两个局限性：

IF-Nets既可以保留输入数据中存在的细节，还能够推理不完整的数据；
IF-Nets能够在复杂服装上重建人体关节。

为此，我们执行了复杂度不断升高的三个实验：

点云补全（Sec0401）
体素超级分辨率（Sec0402）
单视图人体重建（Sec0403）

基线

对于点云补全任务，我们与占用网络（Occupancy Networks，OccNet）[^43]、点集生成网络（Point Set Generation Networks，PSGN）[^15]和深度移动立方体（Deep Marching Cubes，DMC）[^39]进行了对比。
对于体素超级分辨率任务，我们与IMNET[^10]、OccNet和DMC进行了对比。

对于DMC和PSGN，我们使用的是作者在网上提供的实现[^43]。我们训练了所有的方法直到它们出现的是最小检验值。基于每个考虑的实验设置都重复地进行了训练。为了展示一致的比较，我们修改了IMNET的实现从而能够在所有的ShapeNet类别上进行联合训练。对于IMNET和OccNet，我们保持了由方法的作者提出的抽样策略。对于IMNET，我们遵循了作者的方法，在训练期间对训练数据采样执行渐进分辨率增长。

度量

为了定量地评估重建的质量，我们考虑了三个已经建立的度量（详见[^43]中的定义与实现）：

体素IoU（Intersection Over Union，并集相交率）：评估了定义的体积匹配程度（越高越好）；
倒角-（Chamfer）：测量曲面的精确度和完备度（越低越好）；
法向一致性（Normal Consistency）：测量了形状法向的精确度和完备性（越高越好）。

数据

我们考虑了两种数据集：

一种数据集包含了人体的三维扫描数据（从Twindom购买），用于评估不完整的人工关节形状的重建任务；
知名的ShapeNet[^9]数据集，由刚性对象组成，具有相当典型的形状，如：汽车、飞机和步枪。

ShapeNet数据已经被预先由[76]预处理为水密的，这种数据允许计算基准占用，并且缩放每个形状的最大包围盒边界的长度为1。我们在所有的实验和评估中使用预处理的ShapeNet数据，并且都基于[11]进行训练与测试数据的分割。然而，在某些对象中预处理失败，导致输出的对象破碎出现大洞。因此，为了得到有意义的评估，508个严重扭曲的物体被移除。所有使用过的物体的筛选列表与代码一起被发布。

一个具有挑战性的数据集，数据集中包含了扫描得到的人体，人体包含了高度变换的人体关节，关节由复杂的、多变的衣服拓扑（如：外套、裙子、帽子）所包裹。扫描数据是由商业的三维扫描仪也捕获。扫描数据已经在高度上进行了归一化和居中处理，但是相比ShapeNet对象，呈现出了不同的旋转变化。

Sec0401 点云补全

表2：在ShapeNet上点云重建的结果。左边的数字表明基于300个点的得分，右边的数字表明基于3000个点的得分。倒角-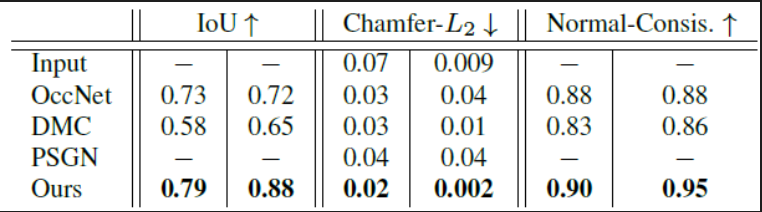
第一个任务，应用IF-Nets到补全稀疏的和稠密的点云问题上，分别从ShapeNet曲面模型中抽样300个点（稀疏）和3000个点（稠密），要求我们的方法补全所有的曲面数据。补全点云极具挑战性，因为它需要在同一时间既保留输入的细节，还推理缺失的结构。在图3中，我们展示了与基线方法的比较，在保留局部细节和恢复全局结构方面都超越了基线。对于稠密点云，我们的优势是显著的。因为只有我们的方法能够重建汽车的一对后视镜和衣柜的附加搁板。我们进一步定量比较了我们的方法及相关的数字（见表2）。我们的方法在所有的度量上大幅度地击败了SOTA。事实上，使用3000个点作为输入，所有竞争者产生的结果都比输入自身的倒角距离要大，表明它们在保留输入细节上是失败的。当补全缺失结构时，仅IF-Nets保留了输入的细节。

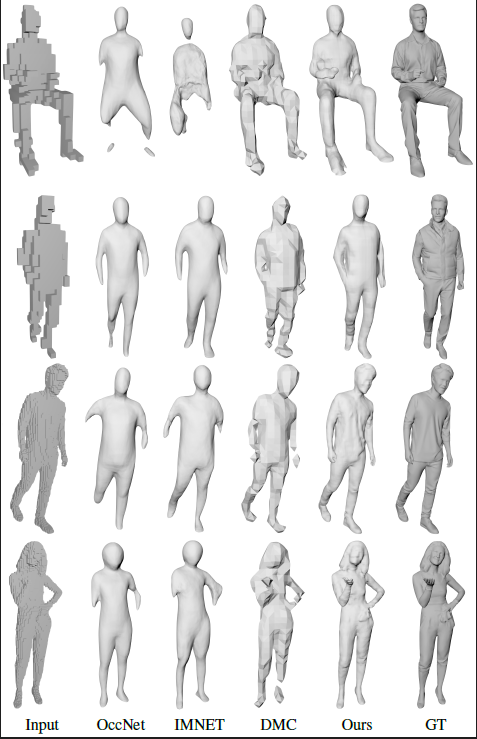
图3：两种输入类别的定性结果：ShapeNet数据集的点云（上）和体素（下）。每个类别都被拆分为稀疏（上两行）和稠密（下两行）。

Sec0402 体素超级分辨率

表3：在ShapeNet上体素网格重建结果。对于每个测度，左列表示的是来自于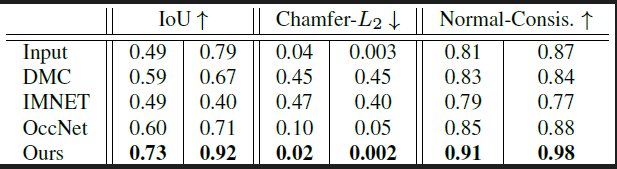

第二个任务，应用我们的方法到三维超级分辨率中。为了有效地解决这个任务，我们的方法需要在输入中不存在重建细节时，再次保留输入的形状。我们的方法在图3（下）中与基线并排地进行了比较。当大部分基线方法要么输出了不存在的结构，要么补全失败，我们的方法仍然一贯地生成了精确的、具有高度细节的结果（具体的数值比较参考表3），并且在所有测度上超越了基线。

图4：基于人体数据集的稀疏（，上面）和稠密（，下面）的3D体素超分辨率的定量结果。

图4中最后两个例子表明了当前隐方法的局限性：如果一个形状与训练集差别较大，当前的这些方法要么失败，要么返回一个与见过的样本相似的结果。结果，我们假定当前的这些方法不适合形状原型分类不充分的任务，人体就是这类问题，因为其需要面对不同的形状和关节。为了验证我们的假设，我们还在人体数据集上进行了三维超级分辨率处理。这个验证展示了更加显著的优势：我们是唯一一种能够持续重建所有肢体，并且还产生高度细节结果的方法。基于隐式学习的基线产生的都是截断的或者完全缺失的肢体。我们在定量分析上也显著地超越了所有基线（见表4）。

表4：在人体数据集上体素网格重建的结果。左列表示的是来自于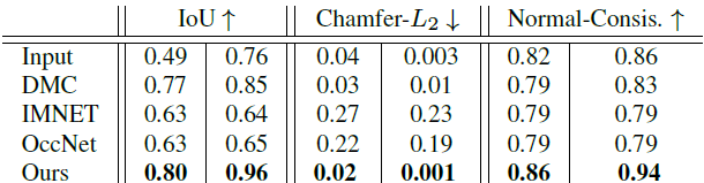

Sec0403 单视图人体重建

最后，为了展示IF-Nets的全部功能，我们在单视图人体重建中应用它们。在这个任务中，输入中仅给出了局部三维点云，这是深度的照相机的典型输出。我们实施这个实验在具有挑战性的人体数据集上，通过渲染一个分辨率的深度图像，产生了大约5000个点在主题的可视面。为了成功地完成这个任务，我们的模型必须同时完成新颖的人体关节重建、保留精细的细节，并且补全遮挡区域的缺失数据（输入中只包含基础形状的一侧）。尽管存在这些挑战，我们的模型能够重建看似合理的和具有高度细节的形状。在图5中，我们从四个不同的角度展示了输入和输出。请注意，像疤痕、皱纹或者单个手指这样的精细结构也出现在重建的形状中。虽然背面区域（被遮挡的部分）相比可见区域的细节更少，但是IF-Nets依然生成了看似合理的曲面。

图5：从点云中实现3D单视角重建（注：背面是完全未知的）。对于四个不同的单视角点云，我们的重建展示了四个不同的视点。

这也可以定量地分析：我们的IoU是、倒角-是、法向一致性。输入点云的倒角-是。定量的结果在的重建质量和完全体素输入之间（见表4），这再次验证了IF-Nets可以补全单视图数据。在补充的视频中，我们展示了从视频中得到的BUFF数据集上[^80]完成单视图重建得到的附加结果（模型无需再次训练或者精调）。

Sec05 讨论和结论

在本文中，我们为有缺陷的三维输入引入了用于三维重建和补全的IF-Nets。首先，我们讨论了一个包含了三维多尺度的深度特征的编码，它与嵌入形状的欧几里德空间对齐。其次，我们不直接对坐标进行分类，而是对在它们的位置提取的深层特征进行分类。实验表明，IF-Nets能够提供连续的输出，可以重建多种拓扑结构，例如：不同服装中的三维人体、ShapeNet的三维对象。定量分析，IF-Nets的性能在所有任务上显著地优于所有SOTA基线。在单视角点云重建中（在可见部分具有细节，在遮挡部分缺失数据）展示了IF-Nets的优势：保留输入中的细节，补全形状的遮挡部分的细节，即使遮挡部分是关节类形状。

未来的工作是探索IF-Nets的泛化性，使其能够对局部输入中细节的假设条件进行采样。我们还计划分两个阶段解决基于图像的重建：首先预测一个深度图，其次使用IF-Nets补全形状。

随着越来越多的计算机视觉重建方法生产了局部三维点云和体素，以及三维扫描和深度相机变得更易得到，在未来三维（有缺陷的和不完整的）数据将会无处不在，而IF-Nets有潜力成为这类数据重建和补全的重要组成部分。

续：补充材料

Sec01 实现的细节

超参数

接下来，给出了论文主体中实验的超参数。关于符号的详细描述，请参考主文档的Sec03。

在所有的实验中，所有点样本的基准占位数为。在训练期间，子样本的大小被和。在所有实验中对于等式（5）中损失的优化，我们使用 Adam 优化器，参数为,,,。

第一个特征栅格的分辨率为用于体素的超分辨率，用于体素的超分辨率，还用于ShapeNet的点云重建，用于单视角重建。

解码器由3个用于人体体素实验的全连接层和4个用于其他实验的全连接层组成。为了在表面的附近采样基准点，我们使用用于 ShapeNet 从 3000 点中重建，用于其他 ShapeNet 实验，用于人体超分辨率，用于单视图重建。

为了沿着 XYZ 轴实现特征提取，我们使用距离用于 ShapeNet 的体素化，用于其他实验。

我们使用类特征栅格用于的人体和 ShapeNet 体素化，用于的人体体素化，用于 ShapeNet 的和 3000 个点，用于单视图重建。代码参考：https://virtualhumans.mpi-inf.mpg.de/ifnets/

连续特征抽取

接下来，我们进一步描述主体论文中的等式（3）。为此，我们简要地回顾一下 IF-Nets 的形状解码（详见论文主体的Sec0302）：给定输入形状的编码器生成形状编码。解码是以逐点的方式完成的，即给定一个查询点及其编码，解码器的任务是分类这个点在形状的内部还是外部。为了这个目的，解码器送入局部和全局特征，这些特征是在点中从编码器中抽取的。为了编码局部近邻信息到点的编码中，哪怕在早期的栅格中（如：小感受野的），我们在查询点的位置本身以及沿着笛卡尔坐标轴距离为的周围点提取特征：

其中，是中心点的距离，是第个笛卡尔坐标单位向量。图1描述了这个采样策略。从局部近邻中采样的附加点描述为绿色点。

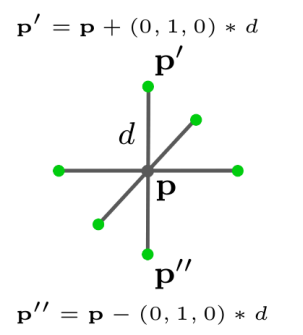
图1：用于特征抽取的定位描述。为了在局部近邻中增加信息到点编码中，我们不仅在查询点本身，还在沿着笛卡尔坐标在距离内的环绕点（绿色点）上抽取特征。

Sec02 人体数据集的水密性

对于我们的人体数据集，为了计算基准占用，我们首先需要全局的水密扫描。因此，不丢失需要的细节则至关重要。为此，我们开发了一种新的水密算法。我们确定隐式空间中3D点的占用值，而不是显式地操作网格。我们称这种方法为隐式水密法。

我们假设，每个物体都像在现实世界中一样拥有一定的厚度。请注意，这种假设对于人体数据集的所有扫描都是成立的，但是有的时候对于仅由人工生成的网格的一个表面表示的薄物体则不能成立。为了计算点在网格的内部还是外部，我们计算穿过平行于其中一个笛卡尔坐标（如图2左中的X坐标）的光线。对于网格内部的点（如：），光线在穿过该点之前必须与表面相交奇数次，并且总共相交偶数次，过程如：光线进入网格，经过该点，然后离开网格。对于网格外的点（如：），光线在穿过该点之前必须与曲面相交偶数次，过程如：光线在通过点之前进入和离开网格。因此，对于没有孔的网格，这种碰撞检测足够计算占用率。现在，考虑一条光线在穿过对应点（如：）之前或者之后遇到表面上的一个孔，于是穿过孔的光线与表面相交的次数为奇数次。现在，我们可以将每个点分为网格内部（绿色）、网格外部（红色）和未知（白色）。参见图2（中）。为了对剩余的未知点进行分类，我们将对象旋转一定的角度，并且对未分类的区域重复分类（图2：右）。这个过程重复多次，直到收敛，剩余的未知点被认定为外部。在人体数据集上，围绕XYZ轴的三次90度旋转足以获得良好的结果。

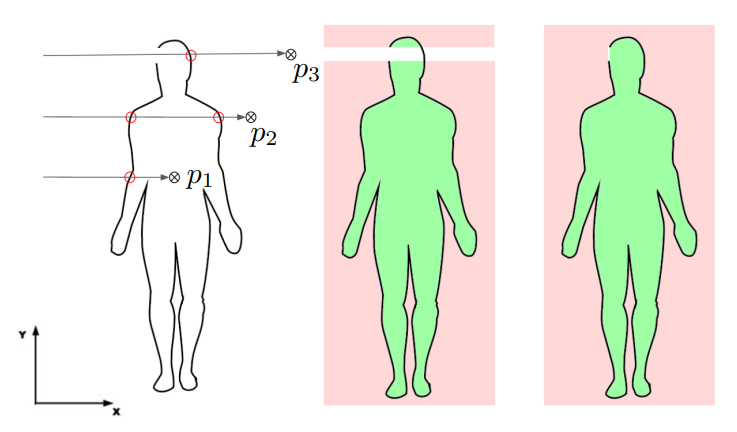
图2：隐式水密算法的可视化。

Sec03 更多结果

单视角人体重建

在图3中，我们展示了从部分点云中重建全身穿衣人体问题的更多定性结果。所有的点云只包含来自于一个视点的数据，并且没有对象背面的信息——典型的深度相机的输出。

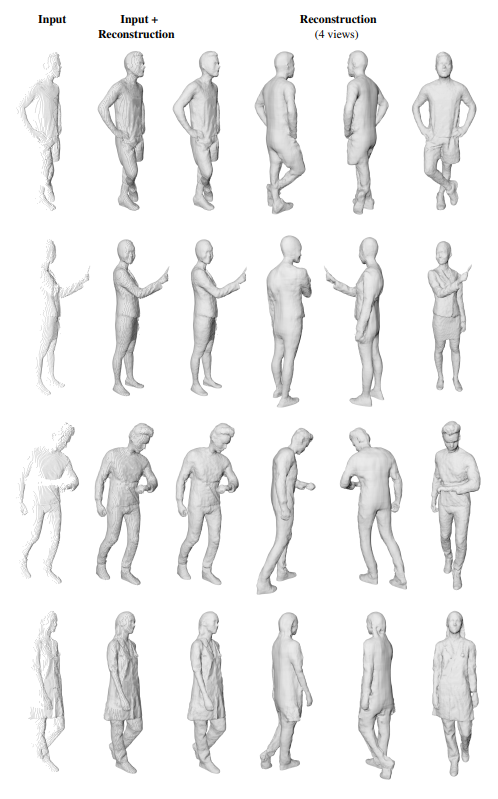
图3：单视角人体重建的更多结果

单视角视频重建

在这个单视角视频重建的附加实验中，我们从BUFF[^2]数据集中重建了一个对象的移动序列。给定的输入是运动人体的单视角点云，其背部被完全遮挡，即：点云仅描述了人的正面。

准确地说，输入是以每秒60帧采集的297帧序列，即大约5秒长。为了众BUFF数据集的4D扫描中生成单视角点云，我们仅使用分辨率，在对象的可视面上生成每帧大约5000个点。将深度像素反向投影到3D空间生成单视角点云。为了这个任务，我们没有在IF-Nets中增加额外的时间约束。相反，我们在逐帧的基础上直接应用来自先前实验的用于单视图重建的训练好的网络。

为了成功地完成这个任务，IF-Nets必须满足静态单视图重建的要求，即：重建未知关节，保留良好的细节，并且同时补全极其不完整的数据。对于这个动态单视图重建任务，IF-Nets增加了测试以展示它们的泛化能力：a)对动态数据（运动）的泛化和b)对训练期间未见的新数据源的泛化。动态数据尤其具有挑战性，因为其重建必须在时间和空间上平滑。

图4、5、6展示了运行序列的9个帧。输入点云在第一列中展示了前视图，在第二列中展示了侧视图。第三列与第四列类似地展示了IF-Nets的重建。详情请参考补充的视频以了解完整的序列重建。

同样，IF-Nets确实保留了输入中存在的细节，如：衣服褶皱、发型或者面部细节。此外，IF-Nets合理地补全了对象的后面。这两个属性都展示了对未见过的数据源的良好的泛化能力。尽管没有对序列数据进行训练，但是将结果序列作为视频观看会展示出令人惊讶的时间平滑重建性能。这个表明，IF-Nets允许连贯地重建单视图视频，同时在服装细节和各种姿势方面具有高度的多样性。

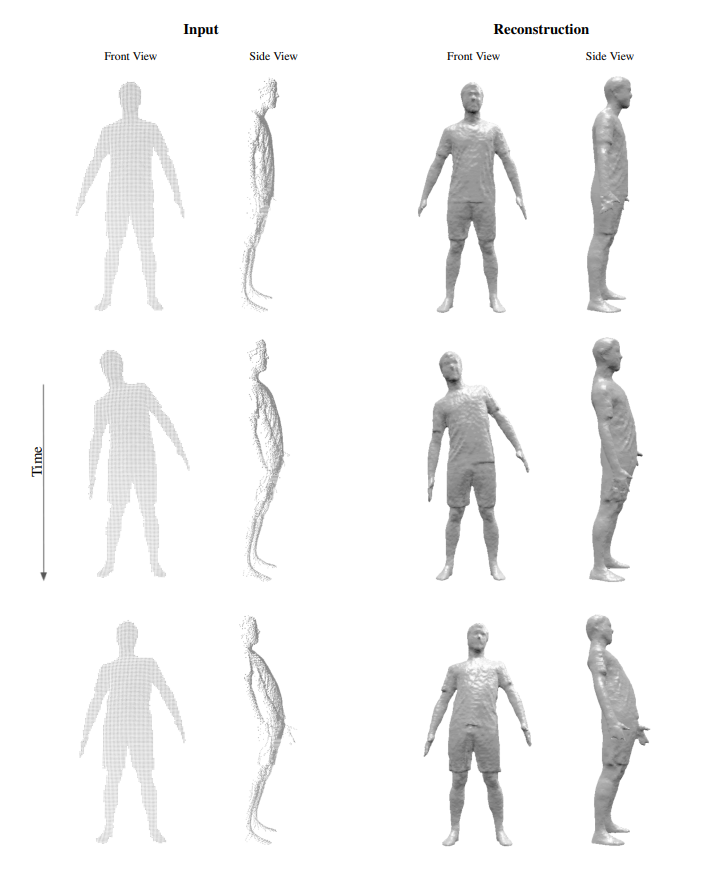
图4：单视角点云和子序列帧的重建（从上到下）。给定的输入从BUFF数据集中（左）提取的一系列运行中的背面完全遮挡的人体单视角点云的序列。重建（右）是逐帧计算的。IF-Nets仅在来自于人体数据集的静态单视图上训练。结果表明，IF-Nets泛化到新的数据源和泛化到训练期间的未知姿势，其生成可以保证时间的一致性。

图5：图4的延续，单视角点云和子序列帧的重建。

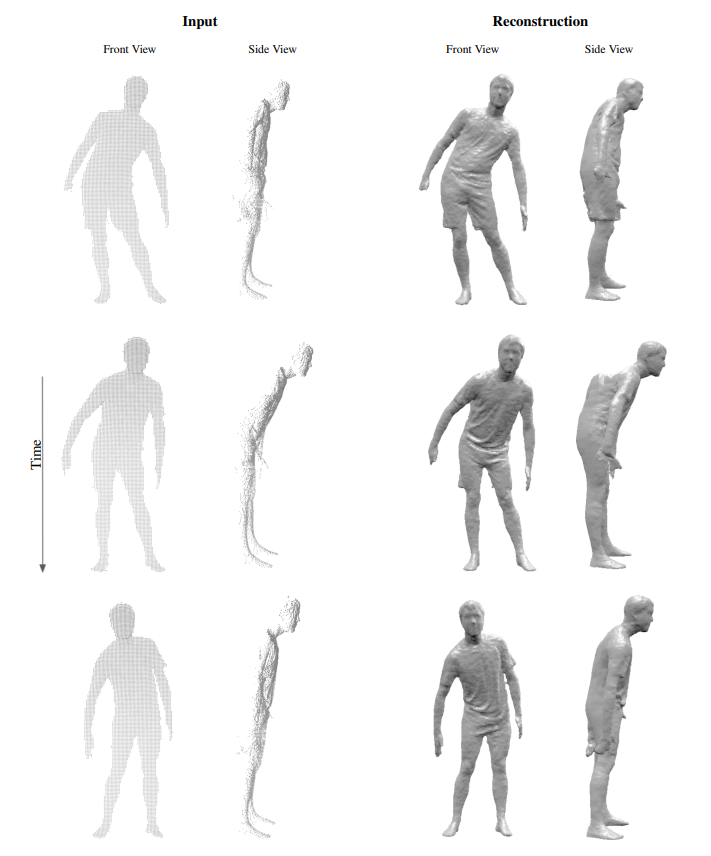
图6：图4、5的延续，单视角点云和子序列帧的重建。

纪要：

特征空间中的隐式函数应用在3D形状的重建和完成

概述

图2：IF-Nets的概览：给定一个（不完整的或者低分辨率的）输入，计算一个多尺度特征的三维网格，编码输入形状的全局和局部性质。然后，在连续点的位置从网格中抽取了深度特征。仅基于抽取的这些特征，解码器判断点是在曲面的内部（类别是1）或者外部（类别是0）。就如最近的基于隐函数的工作，我们可以在任意分辨率下查询，并且重建一个连续曲面。不像以前的方法使用点坐标进行推理，我们的方法仅基于逐点的深度特征。这允许我们去重建关节型结构，并且保留输入的细节。

IF-Nets是编码器-解码器架构。

形状编码

多尺度深度特征网格（Multi-Scale Deep Feature Grid），其中降低的分辨率，每个阶段的通道维度变量。

编码器表示为

形状解码

为了替换直接对点坐标进行分类，我们在位置从特征网格中抽取了学习到的深度特征。

我们的编码具有与输入数据对齐的三维结构，使用三线性插值去查询连续的三维点。

在查询点自身的位置处沿着笛卡尔轴距离为的邻近点提取特征：，其中，是到中心点的距离，是第个笛卡尔坐标轴的单位向量，详见补充材料中的描述。

问题

论文中的问题

三维重建的分类？
- 基于图像的三维重建综述[^23]
- 基于三维输入的三维重建
  - 基于网格的表示：将初始化的凸模板变形，并且不能表示不同的拓扑；
  - 基于体素的表示：占用大量内存，受分辨率的限制，输出的结果缺少细节；
  - 基于点云的表示：效率更高，但是表面渲染和可视化时相对较难。
  - 基于隐函数的表示：在任意分辨率的三维查询点上求值和进行形状恢复，并且输出结果是连续的，可以处理不同的拓扑结果。
- 基于处理的对象分类：刚性对象和人体
  - 刚性对象的体素表示：
    - 受分辨率限制
    - 采用多分辨率方法改善，但是实现复杂
    - 使用截断符号的距离函数（TSDF）[^12]表示形状
    - 具有跳跃连接的层次隐编码表示更大结构的形状
  - 人体的体素表示
    - 从图像的角度，基于体素的表示或者基于深度图的表示，通过CNN实现重建
    - 使用拟合表面多人线性（SMPL）模型进行后处理
  - 刚性对象的网格表示
    - 基于网格的方法将形状预测看作模型的变形，受限于单个拓扑
    - 直接推导出网格（顶点和面片）则计算量非常大，并且不能保证输出没有交集的封闭网格
    - 直接的网格预测可以使用经典的移动立方体算法（MCA）的可学习版本
  - 人体的网格表示
    - 使用SMPL人体模型进行重建，但是模型缺少细节
    - 使用模板进行重建，但是不同的对象需要不同的模板
    - 基于CNN的网格预测往往过于平滑
  - 刚性对象的点云表示：需要后处理进行渲染
    - PointNet思想：将全连接网络应用于每个点，然后执行一个全局池化操作
    - 核化点卷积
    - 基于树的图卷积
    - 规范化流
  - 人体的点云表示
    - 点云表示的研究[^5]很少，可能是渲染不便
    - 网格到点云的对齐
      - PointNet架构
      - 基于点基的架构
  - 刚性对象的隐函数表示
    - 通过神经网络学习表示形状的连续的隐函数，这个隐函数可以输入一个隐编码和一个查询点去预测TSDF值或者点的二进制占用。
    - 将三维查询点特征与局部图像特征相结合，通过视点预测近似地将查询点投影到二维图像中，实现了最先进的三维重建结果
  - 人体的隐函数表示
    - TSDF用于表示人体形状，并且与SMPL人体模型结合起来使用
    - 基于三维查询点和二维图像特征的位置，通过逐点占用预测来实现重建
基于隐函数的表示？
- 关键思想：给定一个编码为向量的粗糙形状，和查询点的坐标，学习一个函数用于决定点在形状的内部还是外部。
- 隐函数的优点：
  - 学习后的隐函数可以在任意分辨率的三维查询点上求值，并且采用经典的移动立方体算法（Marching Cubes Algorithm，MCA）提取网格或者曲面
  - 这种输出表示能够支持以任意的分辨率进行形状恢复，并且输出结果是连续的，可以处理不同的拓扑结果。
- 隐函数的缺点：
  - 不能表示复杂的对象
  - 不能保留输入数据中的细节
IF-Nets的网络特点？
- 保证了输出的连续性
- 处理多种拓扑结构
- 补全稀疏的或者丢失的数据的形状（稀疏输入）
- 保留了隐函数的良好特性
- 保留输入数据中存在的细节信息（稠密输入）
- 更好的重建结果
  - 重建简单的刚性三维对象
  - 全局地重建多关节型人体，而且恢复了细节性结构
IF-Nets与其他方法相比的关键区别？
- 其他方法存在的问题
  - 网络在坐标上学习了的先验，破坏了关节的方差
  - 形状编码向量缺少三维结构，导致解码看起来更像形状原型的分类，而不是连续性的回归
- IF-Nets的改进方法
  - 使用可以通过深度学习得到的三维多尺度张量特征来代替单个向量编码三维形状，并且这个特征对齐了嵌入到形状中的原始的欧几里德空间
  - 使用从连续查询点中抽取的深度特征代替坐标进行分类
    - 原始特征：坐标在欧几里德变换下是任意的（即：可以经过变换得到任意一个位置）
    - 本文特征：围绕着点基于多尺度特征编码局部的和全局的对象形状结构信息
三维多尺度张量特征是什么？
嵌入在形状中的原始的欧几里德空间是什么？
输入的数据是什么？如何与空间对齐？
如何对连续查询点提取的深度特征分类？
输出的效果：是什么？
输入的是点云时，如何进行简单的离散化？是使用占用网络了吗？