自动摘要: 原理 CBCT,即锥形束投照计算机重组断层影像设备(ConeBeamCcomputertomography),其基本原理是采用锥形射线束投照,射线经患者后由平板探测器接收,扫描时X线 ……..
原理
CBCT,即锥形束投照计算机重组断层影像设备(Cone Beam Ccomputertomography),其基本原理是采用锥形射线束投照,射线经患者后由平板探测器接收,扫描时 X 线发生器围绕投照体投照,将所得数据收集在计算机中重组,从而得到三维图像。
与传统 CT 相比,CBCT 用三维锥形束 X 线扫描,获得近 600 个不同的图像,重建后直接得到三维图像,图像金属伪影较轻,而传统 CT 用二维扇形束扫描,重建后形成二维图像数据,伪影较重。

发展
20 世纪 90 年代,第一台口腔专用 CBCT 机 NewTom9000 问世,精确清晰面部三维影像;1996 年该设备进入欧洲市场,1999 年进入中国市场,2001 年进入美国市场。
近年来 CBCT 在口腔科的应用越来越广泛,是目前最有前途和实用性的口腔影像设备;主要应用于口腔种植科、牙体牙髓病科、口腔正畸科、口腔颌面外科、牙周病科等其他口腔科室。

市场
随着口腔 CBCT 渗透率的扩大,存量市场空间进一步扩大。对比来看,台湾有 6000 多家民营口腔诊所,其中 2000-2500 家配备 CBCT,渗透率约 33-42%。而我国大陆 2014 年 CBCT 的保有量仅 1400 台(二维普通牙科 CT 保有量约 7 万台,未来升级换代需求量也较大),在约 6-7 万家口腔诊所中的实际已实现渗透率仅 2%。按现有约 8 万家民营口腔诊所估算,假设 CBCT 市场需求渗透率为 20%,每台价款以 30 万元计算,当前市场存量空间约为 50 亿元。
随着民营口腔诊所的不断扩张,口腔 CBCT 增量市场空间大。再对标台湾,台湾每万人对应 2.6 家民营口腔诊所,那么我国的 8.13 亿城镇人口则需要至少 21 万家,也就是说至少还需要新增 13 万家民营诊所,按照 20% 的 CBCT 渗透率计算,保守估计未来我国口腔 CBCT 机内的刚性需求至少 2.6 万台,按每台 30 万元计算,市场增量空间可实现 80 亿元人民币。
综上,未来我国口腔 CBCT 行业存量加增量市场空间将超百亿元。CBCT 的更新周期取决于关键部件 X 射线探测器的技术突破,平均在 5 年左右,配套软件则快一些,一般 2 年左右会有更新。成本是阻碍小的诊所采购数字化设备和软件的主要原因之一。随着口腔 CBCT 市场渗透率不断提升并稳定下来,按照 5 年更换一次设备来计算,未来市场每年更换空间超 20 亿元。

竞争
目前我国高端口腔 CBCT 设备进口依赖度很高,市场上的主要进口品牌有意大利的 Newtom、德国的卡佤、日本的森田、美国的西诺德、韩国的怡友等;国内口腔 CT 设备厂商主要有美亚光电、北京朗视、博恩登特等。

2012 年以前,国内的口腔 CT 市场完全由国外企业占据,其特点是高品质、高性能、高价格,现在的大型口腔专科医院的 CBCT 基本都是采购国外的,大医院病人量很大,且临床的要求很高,不采购国产设备是因为其还达不到要求。但是随着近年来国产品牌量产带来成本的降低和国内市场竞争程度的提高,国外 CBCT 价格也开始有松动的趋势,国外二三线品牌和国产品牌的 CBCT 主要销往民营口腔机构。
但近年来,在人口老龄化、消费需求升级、进口替代以及政府政策大力支持等因素驱动下,国产医疗器械企业迎来良好的发展契机。例如,美亚光电自主研发的口腔 CBCT 系列产品成功打破了国外产品在高端医疗器械领域的垄断格局,填补了国内空白,使公司成为为数不多的可以与国外进口品牌竞争的民族企业。
数据显示,2013 年,美亚光电口腔 CBCT 实现销量 61 台,实现收入 2213 万元;2017 年口腔 CBCT 实现销量近 1000 台,实现收入 2.6 亿元;2013-2017 年销量年复合增速达 101.22%,销售收入年复合增速达 85.14%。目前,美亚光电生产的口腔 CBCT 在国内市场占有率达到 31.45%。

深度学习研究:
1. 问题
锥形束 CT(CBCT)通过减少 X 射线管阴极电流可以减少对患者的辐射,但是这样重建出来的图像的质量会变差。
2. 传统方法-统计迭代重建法
结论:
统计迭代重建法通过设计不同的正则项来重建,TV 正则项(全变分)能保护边缘和去燥,但是会产生阶梯效应;而 hessian 正则项在抑制阶梯时会让边缘模糊化。
原理:
考虑了投影数据的噪声分布特性,对噪声分布建立模型,通过贝叶斯理论和极大似然估计,构建最小二乘目标函数,并利用图像的先验知识构建正则项。正则项的设计对图像质量影响很大。
3.深度学习方法:
从图像方向:
训练一个端到端神经网络,输入退化的图像,输出高质量的图像;
从算法方向:
用网络改造迭代算法,用网络替换掉迭代算法的一部分,或者用网络替换整个迭代算法。
补充资料:
1. CT成像原理
本质: 衰减系数成像。
相关技术
朗伯比尔定律(Beer-Lambert Law)
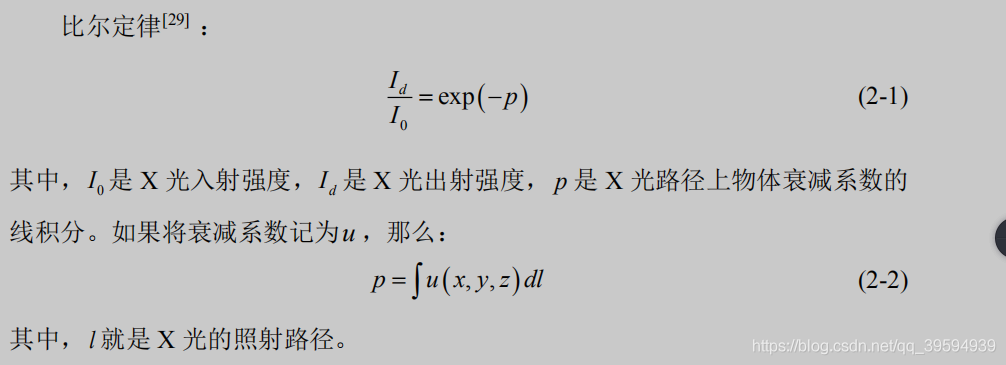

分析:
- 根据 Id 和 I0 得到 p;
- 然后 p 是 u 的线积分,测量多组数据得到 p 的分布;
- 然后就可以得到 u 的分布,
- 根据人体组织与 u 的对应关系,就可以根据 u(x,y,z)得到该位置是什么器官。
拉东变换(Radon transform )
- 使用原因:
比尔定率得出的衰减系数在 X 光穿透路径上是保持不变的。在均匀的物体中穿透没问题,可在非均匀物体中穿透,由于处处的不等,按照这个公式计算出来的 是路径上所有的 的均值。也就是说计算所得的** 不准确。这样的成像效果肯定不会好。三维结构被强制压缩成二维图像,没有空间分辨率,断层效果更差;**
实际上衰减系数是关于空间位置坐标和能量的函数,相同物质对不同能量的吸收能量也不一样,探测器上面检测到的是该路径上所有物质对 x 光吸收后的结果,路径上具体位置的吸收无从得知,这就需要在图像领域朝着各个方向对图像投影(Randon 变换)
- 原理:
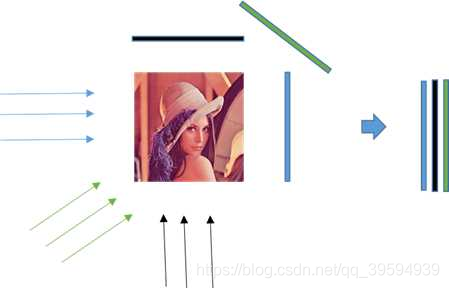
- 如图对图像进行投影(0°,45°,90°),各个方向的投影其实就是计算各个方向上的像素值之和,得到一个向量,
- 把三个方向的投影结果合起来就是投影数据,
- 不同方向得到的向量维数不一样,以最大维数为准,不足用 0 填充,
重建方法
获得图像方法:以螺旋 CT 为例,机器会围绕人作旋转运动,把人看着图像,
- CT 围绕人旋转,那么其发出的 X 光就会从不同角度穿透人体,达到另一面的探测器上。就相当于沿各向求和,
- 这里的和是不同方向上人体对 X 光的吸收作用。探测器就记录下了这个投影数据,后面用来重建人体的三维结构。
获得图像原理:(拉东反变换)
- 水平方向,强度为 10 的 X 光穿透物体后,探测器探测到的结果为 5。只从这一点,我们只知道 μ1+μ2=10-5=5 , 具体μ1,μ2 是多少,无法知晓。
- 但是!从其竖直方向可以得到μ1=10-8=2,μ2=10-7=3 。
- 这就像是联立方程解方程组,就像做数独。实际过程中,几百个方向上的投影来解出每个位置的衰减系数。然后一副二维的切片图像就得出了。
**FDK 等解析类重建算法:**优点:计算效率高,重建速度快
缺点:
- 解析类算法的推导过程中,方程的导出形式是连续的,而且还要满足投影数据必须完全、分布必须均匀、相邻射线等间隔等一系列条件。而实际中,这些条件很难得到满足。
- 连续方程的离散化实现时也会引入插值误差。这些都会导致重建图像有较大的噪声或者伪影,无法得到较好质量的重建图像。
迭代算法:

主要会碰到 A 不可逆以及 A 过于庞大不易存储的问题代数重建问题(线性方程组的应用):这里找到在别人的博文上面对这个问题的介绍:X 射线透视可以得到 3 维对象在 2 维平面上的投影,CT 则通过不同角度的 X 射线得到 3 维对象的多个 2 维投影,并以此重建对象内部的 3 维图像。代数重建方法就是从这些 2 维投影出发,通过求解超定线性方程组,获得对象内部 3 维图像的方法。这里我们考虑一个更简单的模型,从 2 维图像的 1 维投影重建原先的 2 维图像。
一个长方形图像可以用一个横竖均匀划分的离散网格来覆盖,每个网格对应一个像素,它是该网格上各点像素的均值。这样一个图像就可以用一个矩阵表示,其元素就是图像在一点的灰度值(黑白图像)。下面我们以 3*3 图像为例来说明。
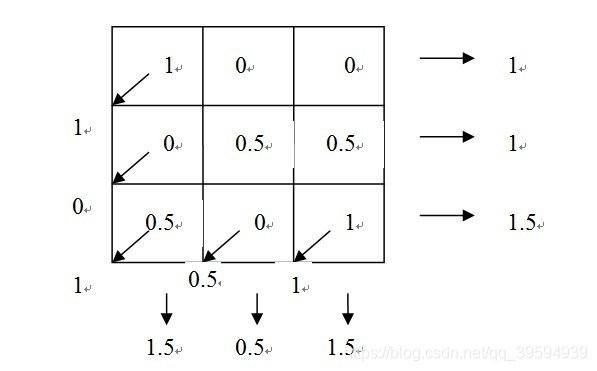
每个网格中的数字代表其灰度值,范围在[0,1]内,记 0 表示白,1 表示黑,0.5 为中间的灰色,沿某个方向的投影就将该方向上的灰度值相加(见上图所示)。如果我们不知道网格中的数值,只知道沿竖直方向和水平方向的投影。设网格按第 1 列、第 2 列、第 3 列的顺序排列,为了确定网格中的灰度值,可以建立线性方程组:
显然该方程组的解是不唯一的,为了重建图像,必须增加投影数量。如我们增加从右上到左下的投影,则方程组将增加 5 个方程,成为超定方程组。考虑到测量误差,可以将超定方程组的近似解作为重建的图像数据。但是在实际情况中在实际情况中,由于噪声的影响,方程组是不相容的,几乎不可能得到唯一解。
统计迭代法,通过贝叶斯法则得到图像 u 的贝叶斯目标函数:
由于投影数据的噪声服从高斯分布,因此可以通过投影数据高斯分布的联合概率密度函数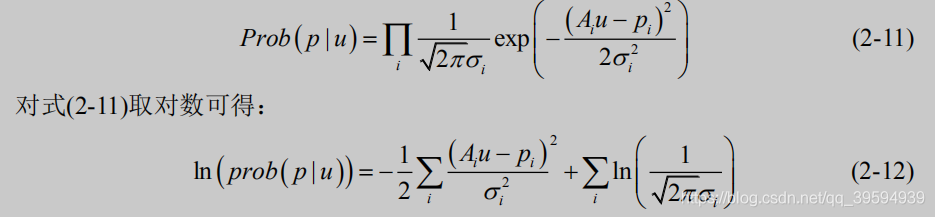
忽略 2-12 的常数项,可以得到惩罚加权最小二乘模型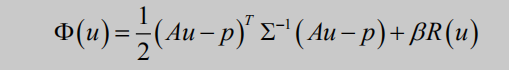
根据最大后验概率理论,上式取最小值的解即为待重建的图像 u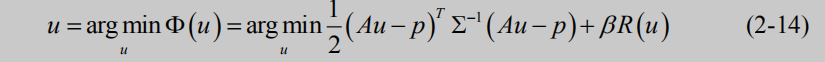
第一项就是保真项,第二项是正则项
正则项方法
①正则项的设计②TV 正则项和 hessian 正则项TV 正则项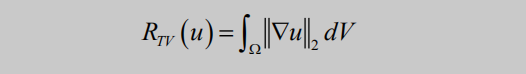

TV 正则项是一种一阶导正则项,它能有效去除重建图像中的伪影和噪声—- 而图像中噪声和伪影附近的梯度通常会较大,也就是灰度值与它相邻点的灰度值相差较大,TV 正则项的权值就会较大,相应的会施加较重的惩罚。但是也会有阶梯效应—–:因为 TV 正则项是对相邻像素之间的灰度差进行惩罚,对于图像灰度均匀变化的区域来说,这种惩罚力度稍微有点强了,导致相邻像素的灰度值趋向于相等。
Hessian 正则项
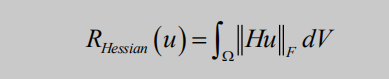

解释一下,F 范数是矩阵中各项元素的绝对值的平方的总和开根号。
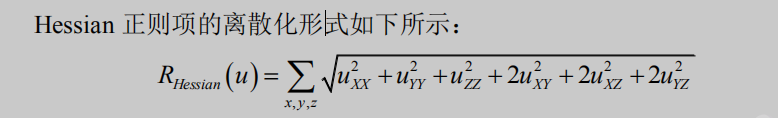

可以看到 hessian 惩罚的相邻像素导数的差值,所以可以有效抑制阶梯效应,但是在图像的边缘处二阶导数一般较大,对其惩罚,可能会使边缘模糊。

